
分析 先设出y=(x-x1)2+(x-x2)2+(x-x3)2+…+(x-xn)2,然后进行整理得出y=nx2-2(x1+x2+x3+…+xn)x+(x12+x22+x32+…+xn2),再求出二次函数的最小值,再根据x的取值即可得出答案.
解答 解:设y=(x-x1)2+(x-x2)2+(x-x3)2+…+(x-xn)2=x2-2xx1+x12+x2-2xx2+x22+x2-2xx3+x32+…+x2-2xxn+xn2=nx2-2(x1+x2+x3+…+xn)x+(x12+x22+x32+…+xn2),
则当x=-$\frac{-2({x}_{1}+{x}_{2}+{x}_{3}+…{x}_{n})}{2n}$=$\frac{{x}_{1}+{x}_{2}+{x}_{3}+…+{x}_{n}}{n}$,
二次函数y=nx2-2(x1+x2+x3+…+xn)x+(x12+x22+x32+…+xn2)最小,
x所取的这个值与平均数有关系.
点评 此题考查了方差和二次函数,关键是设y=(x-x1)2+(x-x2)2+(x-x3)2+…+(x-xn)2,得到一个二次函数,用到的知识点是求二次函数的最小值.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
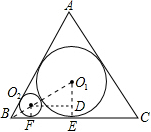 如图,在边长为54$\sqrt{3}$的正三角形ABC中,圆O1为△ABC的内切圆,圆O2与圆O1外切,且与AB、BC相切;圆O3与圆O2外切,且与AB、BC相切…如此继续下去,请计算圆O5的周长为$\frac{2}{3}$π.(结果保留π)
如图,在边长为54$\sqrt{3}$的正三角形ABC中,圆O1为△ABC的内切圆,圆O2与圆O1外切,且与AB、BC相切;圆O3与圆O2外切,且与AB、BC相切…如此继续下去,请计算圆O5的周长为$\frac{2}{3}$π.(结果保留π)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,下列条件中,不能判断直线AB∥CD的是( )
如图,下列条件中,不能判断直线AB∥CD的是( )| A. | ∠HEG=∠EGF | B. | ∠EHF+∠CFH=180° | C. | ∠EHF=∠CFH | D. | ∠AEG=∠DGE |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com