
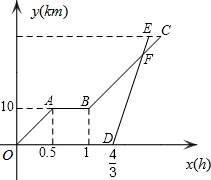
 周末,甲、乙两人从学校出发去公园游玩,甲骑自行车出发0.5小时后到达苏果超市,在超市里休息了一段时间,再以相同的速度前往公园.乙因为一些事情耽搁了一些时间,在甲出发$\frac{4}{3}$小时后,乙驾驶电瓶车沿相同的路线前往公园,如图,是他们离学校的路程y(km)与行走的时间x(h)的函数图象.已知乙驾驶电瓶车的速度是甲骑自行车的2倍.
周末,甲、乙两人从学校出发去公园游玩,甲骑自行车出发0.5小时后到达苏果超市,在超市里休息了一段时间,再以相同的速度前往公园.乙因为一些事情耽搁了一些时间,在甲出发$\frac{4}{3}$小时后,乙驾驶电瓶车沿相同的路线前往公园,如图,是他们离学校的路程y(km)与行走的时间x(h)的函数图象.已知乙驾驶电瓶车的速度是甲骑自行车的2倍.分析 (1)根据图象可以求出甲在苏果超市休息的时间,由速度=路程÷时间就可以求出甲骑车的速度;
(2)直接运用待定系数法就可以求出直线BC和DE的解析式,再由其解析式建立二元一次方程组,求出点F的坐标就可以求出结论.
解答 解:(1)由图象得:甲骑车速度:10÷0.5=20(km/h);
由函数图象得出,在苏果超市休息的时间是1-0.5=0.5h;
(2)乙驾车速度:20×2=40(km/h)
设直线OA的解析式为y=kx(k≠0),
则10=0.5k,
解得:k=20,
故直线OA的解析式为:y=20x.
∵甲走OA段与走BC段速度不变,
∴OA∥BC.
设直线BC解析式为y=20x+b1,
把点B(1,10)代入得b1=-10
∴y=20x-10,
设直线DE解析式为y=40x+b2,把点D($\frac{4}{3}$,0),
代入得:b2=-$\frac{160}{3}$,
∴y=40x-$\frac{160}{3}$.
∴$\left\{\begin{array}{l}{y=20x-10}\\{y=40x-\frac{160}{3}}\end{array}\right.$,
解得:x=$\frac{13}{6}$.
∴F点的横坐标为$\frac{13}{6}$,
$\frac{13}{6}$-$\frac{4}{3}$=$\frac{5}{6}$,
则乙出发$\frac{5}{6}$小时追上甲.
点评 本题考查了一次函数的应用,待定系数法求一次函数的解析式的运用,一次函数图象性质的而运用.解题的关键是从实际问题中整理出一次函数模型.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{{{x^2}-{y^2}}}{x-y}$=x-y | B. | $\frac{{{x^2}-2xy+{y^2}}}{x-y}$=x-y | ||
| C. | $\frac{xy}{{{x^2}-xy}}=\frac{y}{x-y}$ | D. | $\frac{{{y^2}-{x^2}}}{xy}=\frac{y}{x}-\frac{x}{y}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8-4-6+5 | B. | 8-4-6-5 | C. | 8+(-4)+(-6)+5 | D. | 8+4-6-5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | 0.1$\stackrel{•}{0}$$\stackrel{•}{1}$ | C. | $\sqrt{4}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3$\sqrt{2}$ | B. | $\sqrt{32}$ | C. | $\sqrt{24}$ | D. | $\frac{1}{\sqrt{8}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
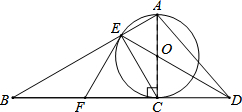 已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF.
已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com