
【题目】2011年国家对“酒后驾车”加大了处罚力度,出台了不准酒后驾车的禁令.某记者在一停车场对开车的司机进行了相关的调查,本次调查结果有四种情况:①偶尔喝点酒后开车;②已戒酒或从来不喝酒;③喝酒后不开车或请专业司机代驾;④平时喝酒,但开车当天不喝酒.将这次调查悄况整理并绘制了如下尚不完整的统计图,请根据相关信息,解答下列问题
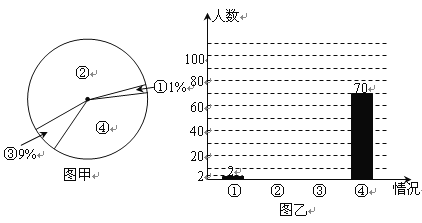
(1)该记者本次一共调查了 名司机.
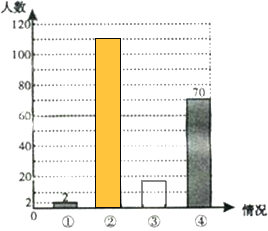
(2)求图甲中④所在扇形的圆心角,并补全图乙.
(3)在本次调查中,记者随机采访其中的一名司机,求他属第②种情况的概率.
【答案】(1)200人(2)126°,18人,110人(3)![]()
【解析】(1)![]() =200(人)总人数是200人.……………………………2分
=200(人)总人数是200人.……………………………2分
(2)![]() ×360°=126°.……………………………4分
×360°=126°.……………………………4分
200×9%=18(人)
200-18-2-70=110(人)
第②种情况110人,第③种情况18人.……………………………6分
(3)他属第②种情况的概率为![]() =
=![]() .…………………………………………8分
.…………………………………………8分
在本次调查中,记者随机采访其中的一名司机.求他属第②种情况的概率![]() .
.
(1)从扇形图可看出①种情况占1%,从条形图知道有2人,所以可求出总人数.
(2)求出④所占的百分比然后乘以360°就可得到圆心角度数,然后求出其他情况的人,补全条形图.
(3)②种情况的概率为②中调查的人数除以调查的总人数.


科目:初中数学 来源: 题型:
【题目】已知:![]() 中,
中,![]() ,求证:
,求证:![]() ,下面写出可运用反证法证明这个命题的四个步骤:
,下面写出可运用反证法证明这个命题的四个步骤:
①∴![]() ,这与三角形内角和为
,这与三角形内角和为![]() 矛盾,②因此假设不成立.∴
矛盾,②因此假设不成立.∴![]() ,③假设在
,③假设在![]() 中,
中,![]() ,④由
,④由![]() ,得
,得![]() ,即
,即![]() .这四个步骤正确的顺序应是( )
.这四个步骤正确的顺序应是( )
A.③④②①B.③④①②C.①②③④D.④③①②
查看答案和解析>>
科目:初中数学 来源: 题型:
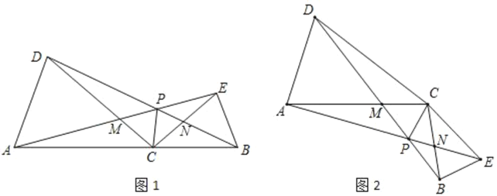
【题目】如图1,点C为线段AB上任意一点(不与点A、B重合),分别以AC、BC为一腰在AB的同侧作等腰△ACD和△BCE,CA=CD,CB=CE,∠ACD=∠BCE=30°,连接AE交CD于点M,连接BD交CE于点N,AE与BD交于点P,连接CP.
(1)线段AE与DB的数量关系为 ;请直接写出∠APD= ;
(2)将△BCE绕点C旋转到如图2所示的位置,其他条件不变,探究线段AE与DB的数量关系,并说明理由;求出此时∠APD的度数;
(3)在(2)的条件下求证:∠APC=∠BPC.
查看答案和解析>>
科目:初中数学 来源: 题型:
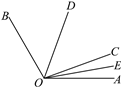
【题目】已知∠AOC和∠BOC,OD平分∠BOC,OE平分∠AOC.
(1)请写出一对相等的角;
(2)若∠AOC在∠BOC的外部,且∠AOB=120°,如图,其他条件不变,求∠EOD的度数.从结果你能看出∠EOD与∠AOB有什么数量关系吗?
(3)若∠AOC=α,∠BOC=β(α,β都大于0°且小于180°,且α<β),其他条件不变,试求∠EOD的度数(结果用含α,β的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017湖北省鄂州市,第8题,3分)小东家与学校之间是一条笔直的公路,早饭后,小东步行前往学校,图中发现忘带画板,停下给妈妈打电话,妈妈接到电话后,带上画板马上赶往学校,同时小东沿原路返回,两人相遇后,小东立即赶往学校,妈妈沿原路返回16min到家,再过5min小东到达学校,小东始终以100m/min的速度步行,小东和妈妈的距离y(单位:m)与小东打完电话后的步行时间t(单位:min)之间的函数关系如图所示,下列四种说法:
①打电话时,小东和妈妈的距离为1400米;
②小东和妈妈相遇后,妈妈回家的速度为50m/min;
③小东打完电话后,经过27min到达学校;
④小东家离学校的距离为2900m.
其中正确的个数是( )
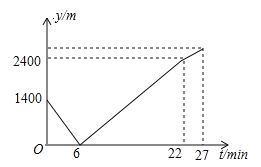
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC=2,以AB为直径的⊙O分别交BC、AC于点D、E,且点D为BC的中点.
(1)求证:△ABC为等边三角形;
(2)求DE的长;
(3)在线段AB的延长线上是否存在一点P,使△PBD≌△AED?若存在,请求出PB的长;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在平面直角坐标系中,作出下列各点,A(-3,4), B(-3,-2),O(0,0),并把各点连起来.
(2)画出△ABO先向下平移2个单位,再向右平移4 个单位得到的图形△A1B1o1,并直接写出A1坐标
(3) 直接写出三角形ABO的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架,书中的算法体系至今仍在推动着计算机的发展和应用.《九章算术》中记载:今有户不知高、广,竿不知长、短.横之不出四尺,从之不出二尺,邪之适出.问户高、广、邪各几何?译文是:今有门不知其高、宽,有竿,不知其长、短,横放,竿比门宽长出![]() 尺;竖放,竿比门高长出
尺;竖放,竿比门高长出![]() 尺;斜放,竿与门对角线恰好相等.问门高、宽、对角线长分别是多少?若设门对角线长为
尺;斜放,竿与门对角线恰好相等.问门高、宽、对角线长分别是多少?若设门对角线长为![]() 尺,则可列方程为__________.
尺,则可列方程为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于关于x的二次函数y=x2-2mx-3,有下列说法:① 它的图象与x轴有两个公共点; ② 如果当x≤1时y随x的增大而减小,则m=1; ③ 如果将它的图象向左平移3个单位后过原点,则m=-1; ④ 如果当x=5时的函数值与x=2012时的函数值相等,则当x=2017时的函数值为-3.其中正确的说法有______.(填序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com