【题目】经测算，某地气温
与距离地面的高度
有如下对应关系：
| 0 | 1 | 2 | 3 | 4 | 5 | … |
| 26 | 20 | 14 | 8 |
| -4 | … |
请根据上表，完成下面的问题.
（1）猜想：距离地面的高度每上升
，气温就下降______
；表中
______.
（2）气温
与高度
之间的函数关系式是______.
（3）求该地距离地面
处的气温.
科目：初中数学 来源： 题型：
【题目】如图，在等腰△ABC中，AB＝AC＝3cm，∠B＝30°，点D在BC边上由C向B匀速运动（D不与B、C重合），匀速运动速度为1cm/s，连接AD，作∠ADE＝30°，DE交线段AC于点E．
（1）在此运动过程中，∠BDA逐渐变 （填“大”或“小”）；D点运动到图1位置时，∠BDA＝75°，则∠BAD＝ ．
（2）点D运动3s后到达图2位置，则CD＝ ．此时△ABD和△DCE是否全等，请说明理由；
（3）在点D运动过程中，△ADE的形状也在变化，判断当△ADE是等腰三角形时，∠BDA等于多少度（请直接写出结果）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知
是等边三角形，
是
上一点，
绕点
逆时针旋转到
的位置．
（1）如图，旋转中心是 ，
；
（2）如图，如果
是
的中点，那么经过上述旋转后，点 转动了 度；
（3）如果点为边上的三等分点，且的面积为
，那么四边形
的面积为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知直线AB：y=kx﹣2（k≠0）与反比例函数的图象相交于点A和点B（﹣4，2），直线l的解析式为：y=
x+b．
（1）求反比例函数和直线AB的解析式；
（2）若直线l恰好与反比例函数的图象仅仅交于一个点，求直线l的解析式；
（3）在（2）的条件下，如图，若直线l与反比例函数的图象交于第四象限的点C，求△ABC的面积．
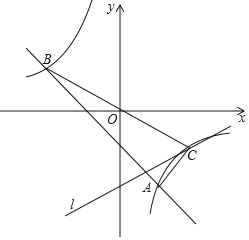
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】探究与发现：在△ABC中，∠B＝∠C，点D在BC边上(点B、C除外)，点E在AC边上，且∠ADE＝∠AED，连接DE.
(1)如图①，若∠B＝∠C＝45，
①当∠BAD＝60时，求∠CDE的度数；
②试猜想∠BAD与∠CDE的数量关系，并说明理由.
(2)深入探究：如图②，若∠B＝∠C，但∠C≠45，其他条件不变，试探究∠BAD与∠CDE的数量关系.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AC=6
,BC的中点为D,将△ABC绕点C顺时针旋转任意一个角度得到△FEC,EF的中点为G,连接DG在旋转过程中,DG的最大值是_______.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知正方形 ABCD 的边长为 10，E 在 BC 边上运动，取 DE 的中点 G，EG 绕点 E 顺时针旋转90°得 EF，问 CE 长为多少时，A、C、F 三点在一条直线上（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC是等腰三角形，且AC=BC，∠ACB=120°，在AB上取一点O，使OB=OC，以O为圆心，OB为半径作圆，过C作CD∥AB交⊙O于点D，连接BD．
（1）猜想AC与⊙O的位置关系，并证明你的猜想；
（2）已知AC=6，求扇形OBC围成的圆锥的底面圆半径．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
