【题目】在甲、乙两名同学中选拔一人参加“中华好诗词”大赛，在相同的测试条件下，两人
次测试成绩(单位：分)如下：
甲：
，
，
，
，
乙：
，，
，
，
．
回答下列问题：
(1)甲成绩的平均数是 ，乙成绩的平均数是 ；
(2)如果从甲、乙两人次的成绩中各随机抽取一次成绩进行分析，求抽到的两个人的成绩都大于
分的概率.(用列表或画树状图的方法)
【答案】(1)
；
；(2)抽到的两个人的成绩都大于
分的概率为
.
【解析】
（1）根据平均数的定义可列式计算；
（2）列表表示出所有等可能的结果，找到能使该事件发生的结果数，根据概率公式计算可得．
(1) 甲成绩的平均数=(79+86+82+85+835) ÷5=83（分），
乙成绩的平均数=(88+79+90+81+725) ÷5=82（分）；
(2)列表如下
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
由表格可知，所有等可能结果共
种，其中两人成绩都大于
分有
种，
∴抽到的两个人的成绩都大于分的概率为
.
或树状图如图：
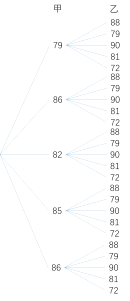
由树状图可知，所有等可能结果共种，其中两人成绩都大于分有种，
抽到的两个人的成绩都大于分的概率为.
心算口算巧算一课一练系列答案科目：初中数学 来源： 题型：
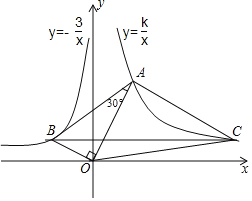
【题目】如图，已知∠AOB=90°，∠OAB=30°，反比例函数
的图象过点
，反比例函数
的图象过点A
（1）求
和
的值.
（2）过点B作BC∥x轴，与双曲线
交于点C，求△OAC的面积.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】求解体验：
（1）已知抛物线 y＝﹣x2+bx﹣3 经过点（﹣1，0），则 b＝ ，顶点坐标为 ，该抛物线关于点（0，1）成中心对称的抛物线表达式是 ．
抽象感悟：
我们定义：对于抛物线 y＝ax2+bx+c（a≠0），以 y 轴上的点 M（0，m）为中心，作该抛物线关于点 M 对称的 抛物线 y′，则我们又称抛物线 y′为抛物线 y 的“衍生抛物线”，点 M 为“衍生中心”．
（2）已知抛物线 y＝﹣x2﹣2x+5 关于点（0，m）的衍生抛物线为 y′，若这两条抛物线有交点，求 m 的取值范 围．
问题解决：
（3）已知抛物线 y＝ax2+2ax﹣b（a≠0）
①若抛物线 y 的衍生抛物线为 y′＝bx2﹣2bx+a2（b≠0），两抛物线有两个交点，且恰好是它们的顶点，求 a、b 的值及衍生中心的坐标；
②若抛物线 y 关于点（0，k+12）的衍生抛物线为 y1，其顶点为 A1；关于点（0，k+22）的衍生抛物线为 y2，其顶点为 A2；…；关于点（0，k+n2）的衍生抛物线为 yn，其顶点为 An…（n 为正整数）．求 An An+1 的长（用含 n 的式子表示）．
查看答案和解析>>
科目：初中数学 来源： 题型：
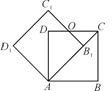
【题目】如图，边长为1的正方形ABCD绕点A逆时针旋转45°得到正方形AB1C1D1，边B1C1与CD交于点O，则四边形AB1OD的面积是（____）
查看答案和解析>>
科目：初中数学 来源： 题型：
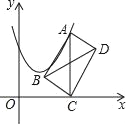
【题目】如图，在平面直角坐标系中，点A在抛物线y＝x2﹣2x+2上运动．过点A作AC⊥x轴于点C，以AC为对角线作矩形ABCD，连结BD，则对角线BD的最小值为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】抛物线y＝ax2+bx+c上部分点的横坐标x，纵坐标y的对应值如下表：
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知，下列说法中正确的是（ ）
A. 抛物线与x轴的一个交点为（4，0）
B. 函数y＝ax2+bx+c的最大值为6
C. 抛物线的对称轴是x＝
D. 在对称轴右侧，y随x增大而增大
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】设a、b是任意两个实数，用max{a，b}表示a、b两数中较大者，例如：max{﹣1，﹣1}=﹣1，max{1，2}=2，max{4，3}=4，参照上面的材料，解答下列问题：
（1）max{5，2}= ，max{0，3}= ；
（2）若max{3x+1，﹣x+1}=﹣x+1，求x的取值范围；
（3）求函数
与y=﹣x+2的图象的交点坐标，函数的图象如图所示，请你在图中作出函数y=﹣x+2的图象，并根据图象直接写出max{﹣x+2，
}的最小值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，抛物线y＝ax2+bx﹣3经过点A，B，C，已知点A（﹣1，0），点B（3，0）
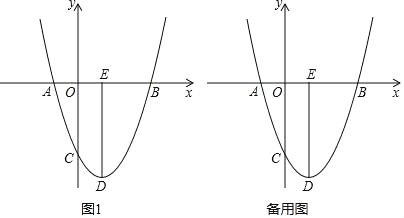
（1）求抛物线的解析式
（2）点D为抛物线的顶点，DE⊥x轴于点E，点N是线段DE上一动点
①当点N在何处时，△CAN的周长最小？
②若点M（m，0）是x轴上一个动点，且∠MNC＝90°，求m的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
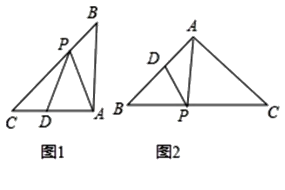
【题目】如图1，在△ABC中，在BC边上取一点P，在AC边上取一点D，连AP、PD，如果△APD是等腰三角形且△ABP与△CDP相似，我们称△APD是AC边上的“等腰邻相似三角形”.
(1)如图2,在△ABC中AB=AC,∠B=50°，△APD是AB边上的“等腰邻相似三角形”，且AD=DP，∠PAC=∠BPD，则∠PAC的度数是___；
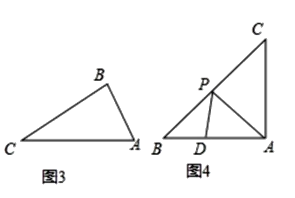
(2)如图3，在△ABC中，∠A=2∠C，在AC边上至少存在一个“等腰邻相似△APD”，请画出一个AC边上的“等腰邻相似△APD”，并说明理由；
(3)如图4，在Rt△ABC中AB=AC=2，△APD是AB边上的“等腰邻相似三角形”，请写出AD长度的所有可能值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
