
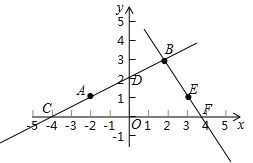
����Ŀ������AB��ֱ��AB��x�ύ�ڵ�C����y�ύ�ڵ�D��ƽ������һ��E��3��1����ֱ��BE��x�ύ�ڵ�F��ֱ��AB�Ľ���ʽ����y1=kx+b��ֱ��BE����ʽ����y2=mx+t����
��1��ֱ��AB�Ľ���ʽ��BCF�������
��2����x ʱ��kx+b��mx+t��
��x ʱ��kx+b��mx+t��
��x ʱ��kx+b=mx+t��
��3����x������һ����H��ʹ����OBHΪ���������Σ���H�����꣮
���𰸡���1��![]() ����2����2����2��=2����3����-
����2����2����2��=2����3����-![]() ��0������
��0������![]() ��0������4��0����
��0������4��0����![]() ��0����
��0����
��������
�����������1�����ݹ۲�ͼ������ҳ���B��C��D�����꣬���ݴ���ϵ�����������ֱ��AB��BE�Ľ���ʽ����y2=0���������F�����꣬��������ε������ʽ���ɵó����ۣ�
��2����ֱ��AB��ͼ����ֱ��BEͼ���Ϸ�ʱ����kx+b��mx+t����ֱ��AB��ͼ����ֱ��BEͼ���·�ʱ����kx+b��mx+t�������ཻʱ����kx+b=mx+t�����ͼ�ɵó����ۣ�
��3�����H������Ϊ��n��0�����������ľ��빫ʽ�ҳ�OB��OH��BH�ij��ȣ������OBHΪ���������ε�����������������n��ֵ��
�����������1���۲캯��ͼ���֪��
��C��-4��0������D��0��2������B��2��3����
��C��D���������ֱ��AB�Ľ���ʽ�У���![]() ��
��
��ã�![]() ��
��
��ֱ��AB�Ľ���ʽΪy1=![]() x+2��
x+2��
����B��2��3����E��3��1�����뵽ֱ��BE�Ľ���ʽ�У���![]() ��
��
��ã�![]() ��
��
��ֱ��BE�Ľ���ʽΪy2=-2x+7��
��y2=0������-2x+7=0�����m=![]() ��
��
����F��������![]() ��0����
��0����
��CF=![]() -��-4��=
-��-4��=![]() ��
��
���BCF�����S=![]() ��3CF=
��3CF=![]() ��3��
��3��![]() =
=![]() ��
��
��2����Ϻ���ͼ���֪��
��x��2ʱ��kx+b��mx+t����x��2ʱ��kx+b��mx+t����x=2ʱ��kx+b=mx+t��
��3�����H��������n��0����
����O��0��0������B��2��3����
��OB=![]() ��OH=|n|��BH=
��OH=|n|��BH=![]() ��
��
��OBH������������������
����OB=OHʱ����![]() =|n|����ã�n=��
=|n|����ã�n=��![]() ��
��
��ʱ��H������Ϊ��-![]() ��0����
��0����![]() ��0����
��0����
����OB=BHʱ����![]() =
=![]() ����ã�n=0����ȥ������n=4��
����ã�n=0����ȥ������n=4��
��ʱ��H������Ϊ��4��0����
����OH=BHʱ����|n|=![]() ����ã�n=
����ã�n=![]() ��
��
��ʱ��H������Ϊ��![]() ��0����
��0����
���Ͽ�֪����H������Ϊ��-![]() ��0������
��0������![]() ��0������4��0����
��0������4��0����![]() ��0����
��0����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���������x�ύ�ڵ�A����1��0���͵�B��1��0����ֱ��y=2x��1��y�ύ�ڵ�C���������߽��ڵ�C��D��
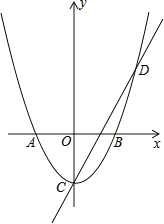
��1���������ߵĽ���ʽ��
��2�����A��ֱ��CD�ľ��룻
��3��ƽ�������ߣ�ʹ�����ߵĶ���P��ֱ��CD�ϣ���������ֱ��CD����һ������ΪQ����G��y���������ϣ�����G��P��Q����Ϊ�����������Ϊ����ֱ��������ʱ��������з���������G������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��������x��ƽ������2a�D3��5-a����x��ֵΪ����
A. �D7 B. 7 C. 49 d.14
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��Բ�ֳ��ĸ����Σ����ǵ�Բ�ĽǵĶ�����Ϊ2��4��5��7����������ε�Բ�Ľ��� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC�У�AB��AC����֤����B��90��.�÷�֤��֤������һ���Ǽ���_________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������⡰��ֱ��ͬ�Dֱ�ߵ�����ֱ����ƽ�С���д�ɡ����������ô��������ʽΪ_____________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��AB��CD����C�ڵ�D���Ҳ࣬��ABC ����ADC��ƽ���߽��ڵ�E������B��D���غϣ�����ABC��n�㣬��ADC��80��.
��1������B�ڵ�A����࣬����BED�Ķ������ú�n�Ĵ���ʽ��ʾ����
��2������1���е��߶�BC��DC����ƽ�ƣ�����B�ƶ�����A�Ҳ�ʱ���뻭��ͼ�β��ж���BED�Ķ����Ƿ�ı�.���ı䣬�������BED�Ķ������ú�n�Ĵ���ʽ��ʾ���������䣬��˵������.

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com