
如图,在△ABC中,∠BAC=90°,AB=9,AC=12,AD⊥BC,垂足为D.

(1)求BC的长;(2)求BD的长.
(1)15(2)
【解析】
试题分析:(1)由已知在△ABC中,∠BAC=90°,所以得到△ABC为直角三角形且AB、AC为两直角边,因此根据勾股定理可求出BC的长.(2)AD⊥BC,垂足为D,所以得到直角三角形DBA,∠BDA和∠BAC都为直角,∠B为公共角,得到△ABC与△DBA相似,根据相似三角形的性质求得BDA.
【解析】
(1)在△ABC中,∵∠BAC=90°,
∴BC2=AB2+AC2(勾股定理),
=92+122,
=81+144,
=225.
∴BC=15.
(2)AD⊥BC,垂足为D,
∴△DBA为直角三角形,
在△ABC与△DBA中,
∠BDA=∠BAC=90°,∠B=∠B(公共角),
∴△ABC∽△DBA,
∴ =
= ,
,
∴BD=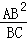 =
= =
= .
.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:初中数学 来源:2015年课时同步练习(浙教版)八年级上2.8直角三角形全等的判定(解析版) 题型:解答题
如图,AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,且DB=DC,求证:EB=FC.
查看答案和解析>>
科目:初中数学 来源:2015年课时同步练习(浙教版)八年级上2.8直角三角形全等的判定(解析版) 题型:选择题
如图,要用“HL”判定Rt△ABC和Rt△A′B′C′全等的条件是( )

A.AC=A′C′,BC=B′C′ B.∠A=∠A′,AB=A′B′
C.AC=A′C′,AB=A′B′ D.∠B=∠B′,BC=B′C′
查看答案和解析>>
科目:初中数学 来源:2015年课时同步练习(浙教版)八年级上2.8直角三角形全等的判定(解析版) 题型:选择题
下列条件不可以判定两个直角三角形全等的是( )
A.两条直角边对应相等 B.有两条边对应相等
C.一条边和一锐角对应相等 D.一条边和一个角对应相等
查看答案和解析>>
科目:初中数学 来源:2015年课时同步练习(浙教版)八年级上2.7探索勾股定理(解析版) 题型:填空题
如图,在Rt△ABC中,∠A=90°,AB=AC=4 ,点D为AC的中点,点E在边BC上,且ED⊥BD,则△CDE的面积是 .
,点D为AC的中点,点E在边BC上,且ED⊥BD,则△CDE的面积是 .

查看答案和解析>>
科目:初中数学 来源:2015年课时同步练习(浙教版)八年级上2.7探索勾股定理(解析版) 题型:填空题
如图,是5×5的正方形网络,方格纸中△ABC的3个顶点分别在小正方形的顶点(格点)上,这样的三角形叫格点三角形,如果以点D、E为两个顶点作位置不同的格点三角形,使所作的格点三角形与△ABC全等,那么,这样的格点三角形最多可以画出 个.

查看答案和解析>>
科目:初中数学 来源:2015年课时同步练习(浙教版)八年级上2.4等腰三角形的判定定理2(解析版) 题型:解答题
已知:如图,在△ABC中,CD⊥AB垂足为D,BE⊥AC垂足为E,连接DE,点G、F分别是BC、DE的中点.
求证:GF⊥DE.

查看答案和解析>>
科目:初中数学 来源:2015年课时同步练习(浙教版)八年级上2.4等腰三角形的判定定理1(解析版) 题型:?????
在等边△ABC所在平面内找出一个点,使它与三角形中的任意两个顶点所组成的三角形都是等腰三角形.这样的点一共有( )
A.1个 B.4个 C.7个 D.10个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com