
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象相交,其中一个交点的横坐标是2.
的图象相交,其中一个交点的横坐标是2.
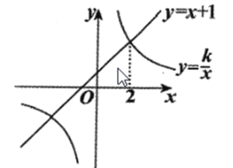
(1)求反比例函数的表达式;
(2)将一次函数![]() 的图象向下平移2个单位,求平移后的图象与反比例函数
的图象向下平移2个单位,求平移后的图象与反比例函数![]() 图象的交点坐标;
图象的交点坐标;
(3)直接写出一个一次函数,使其过点![]() ,且与反比例函数
,且与反比例函数![]() 的图象没有公共点.
的图象没有公共点.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() (答案不唯一)
(答案不唯一)
【解析】
(1)将x=2代入一次函数,求出其中一个交点是![]() ,再代入反比例函数
,再代入反比例函数![]() 即可解答;
即可解答;
(2)先求出平移后的一次函数表达式,联立两个函数解析式得到一元二次方程![]() 即可解答;
即可解答;
(3)设一次函数为y=ax+b(a≠0),根据题意得到b=5,联立一次函数与反比例函数解析式,得到![]() ,若无公共点,则方程无解,利用根的判别式得到
,若无公共点,则方程无解,利用根的判别式得到![]() ,求出a的取值范围,再在范围内任取一个a的值即可.
,求出a的取值范围,再在范围内任取一个a的值即可.
解:(1)∵一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象的一个交点的横坐标是2,
的图象的一个交点的横坐标是2,
∴当![]() 时,
时,![]() ,
,
∴其中一个交点是![]() .
.
∴![]() .
.
∴反比例函数的表达式是![]() .
.
(2)∵一次函数![]() 的图象向下平移2个单位,
的图象向下平移2个单位,
∴平移后的表达式是![]() .
.
联立![]() 及
及![]() ,可得一元二次方程
,可得一元二次方程![]() ,
,
解得![]() ,
,![]() .
.
∴平移后的图象与反比例函数图象的交点坐标为![]()
(3)设一次函数为y=ax+b(a≠0),
∵经过点![]() ,则b=5,
,则b=5,
∴y=ax+5,
联立y=ax+5以及![]() 可得:
可得:![]() ,
,
若一次函数图象与反比例函数图象无交点,
则![]() ,解得:
,解得:![]() ,
,
∴![]() (答案不唯一).
(答案不唯一).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某市总预算![]() 亿元用三年时间建成一条轨道交通线.轨道交通线由线路敷设、搬迁安置、辅助配套三项工程组成.从2015年开始,市政府在每年年初分别对三项工程进行不同数额的投资.
亿元用三年时间建成一条轨道交通线.轨道交通线由线路敷设、搬迁安置、辅助配套三项工程组成.从2015年开始,市政府在每年年初分别对三项工程进行不同数额的投资.
2015年年初,对线路敷设、搬迁安置的投资分别是辅助配套投资的2倍、4倍.随后两年,线路敷设投资每年都增加![]() 亿元,预计线路敷设三年总投资为54亿元时会顺利如期完工;搬迁安置投资从2016年初开始遂年按同一百分数递减,依此规律,在 2017年年初只需投资5亿元,即可顺利如期完工;辅助配套工程在2016年年初的投资在前一年基础上的增长率是线路敷设2016年投资增长率的1.5倍,2017年年初的投资比该项工程前两年投资的总和还多4亿元,若这样,辅助配套工程也可以如期完工.经测算,这三年的线路敷设、辅助配套工程的总投资资金之比达到3: 2.
亿元,预计线路敷设三年总投资为54亿元时会顺利如期完工;搬迁安置投资从2016年初开始遂年按同一百分数递减,依此规律,在 2017年年初只需投资5亿元,即可顺利如期完工;辅助配套工程在2016年年初的投资在前一年基础上的增长率是线路敷设2016年投资增长率的1.5倍,2017年年初的投资比该项工程前两年投资的总和还多4亿元,若这样,辅助配套工程也可以如期完工.经测算,这三年的线路敷设、辅助配套工程的总投资资金之比达到3: 2.
(1)这三年用于辅助配套的投资将达到多少亿元?
(2)市政府2015年年初对三项工程的总投资是多少亿元?
(3)求搬迁安置投资逐年递减的百分数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂将![]() 四种型号的空调销售额的情况绘制成了图①和图②两幅尚不完整的统计图.
四种型号的空调销售额的情况绘制成了图①和图②两幅尚不完整的统计图.
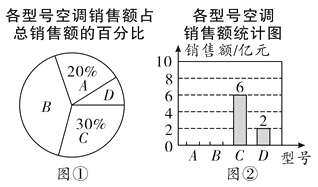
(1)请补全图②的条形统计图;
(2)为了应对激烈的市场竞争,该厂决定降价促销,![]() 四种型号的空调分别降价
四种型号的空调分别降价![]() ,因此该厂宣称其产品平均降价
,因此该厂宣称其产品平均降价![]() ,你认为该厂的说法正确吗?请通过计算说明理由;
,你认为该厂的说法正确吗?请通过计算说明理由;
(3)为进一步促销,该厂决定从这四种型号的空调中任意选取两种型号的空调降价销售,请用树状图或列表法求出降价空调中含D型号空调的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,扇形OAB中,∠AOB=100°,OA=12,C是OB的中点,CD⊥OB交![]() 于点D,以OC为半径的
于点D,以OC为半径的![]() 交OA于点E,则图中阴影部分的面积是( )
交OA于点E,则图中阴影部分的面积是( )

A. 12π+18![]() B. 12π+36
B. 12π+36![]() C. 6π+18
C. 6π+18![]() D. 6π+36
D. 6π+36![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 是正方形,点
是正方形,点![]() 为对角线
为对角线![]() 的中点.
的中点.
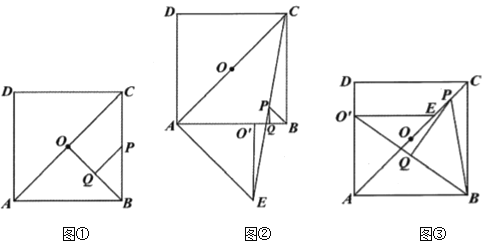
(1)问题解决:如图①,连接![]() ,分别取
,分别取![]() ,
,![]() 的中点
的中点![]() ,
,![]() ,连接
,连接![]() ,则
,则![]() 与
与![]() 的数量关系是_____,位置关系是____;
的数量关系是_____,位置关系是____;
(2)问题探究:如图②,![]() 是将图①中的
是将图①中的![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 得到的三角形,连接
得到的三角形,连接![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,连接
的中点,连接![]() ,
,![]() .判断
.判断![]() 的形状,并证明你的结论;
的形状,并证明你的结论;
(3)拓展延伸:如图③,![]() 是将图①中的
是将图①中的![]() 绕点
绕点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 得到的三角形,连接
得到的三角形,连接![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,连接
的中点,连接![]() ,
,![]() .若正方形
.若正方形![]() 的边长为1,求
的边长为1,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC,∠ABC=90°,顶点A在第一象限,B、C在x轴的正半轴上(C在B的右侧),BC=3,AB=4,若双曲线![]() 交边AB于点E,交边AC于中点D.
交边AB于点E,交边AC于中点D.
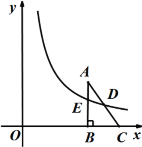
(1)若OB=2,求k;
(2)若AE=![]() , 求直线AC的解析式.
, 求直线AC的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①是甘肃省博物馆的镇馆之宝——铜奔马,又称“马踏飞燕”,于1969年10月出土于武威市的雷台汉墓,1983年10月被国家旅游局确定为中国旅游标志,在很多旅游城市的广场上都有“马踏飞燕”雕塑,某学习小组把测量本城市广场的“马踏飞燕”雕塑(图②)最高点离地面的高度作为一次课题活动,同学们制定了测量方案,并完成了实地测量,测得结果如下表:
课题 | 测量“马踏飞燕”雕塑最高点离地面的高度 | |||
测量示意图 |
| 如图,雕塑的最高点 | ||
测量数据 |
|
|
| 仪器 |
|
| 5米 |
| |
请你根据上表中的测量数据,帮助该小组求出“马踏飞燕”雕塑最高点离地面的高度(结果保留一位小数).(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2﹣ax﹣2a(a为常数且不等于0)与x轴的交点为A,B两点,且A点在B的右侧.
(1)当抛物线经过点(3,8),求a的值;
(2)求A、B两点的坐标;
(3)若抛物线的顶点为M,且点M到x轴的距离等于AB的3倍,求抛物线的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com