
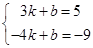 ,
,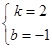 ,
,

 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
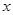 轴的平行线交直线y=0.5x+1于点B1,过点 B1作
轴的平行线交直线y=0.5x+1于点B1,过点 B1作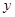 轴的平行线交直线y=x+2于点A1,再过点
轴的平行线交直线y=x+2于点A1,再过点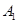 作
作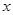 轴的平行线交直线y=0.5x+1于点B2,过点 B2作
轴的平行线交直线y=0.5x+1于点B2,过点 B2作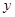 轴的平行线交直线y=x+2于点A2,…,依此类推,得到直线y=x+2上的点A1,A2,A3,…,与直线y=0.5x+1上的点B1,B2,B3,…,则A7B8的长为( )
轴的平行线交直线y=x+2于点A2,…,依此类推,得到直线y=x+2上的点A1,A2,A3,…,与直线y=0.5x+1上的点B1,B2,B3,…,则A7B8的长为( )
| A.64 | B.128 | C.256 | D.512 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.y1>y2 | B.y1>y2>0 | C.y1<y2 | D.y1=y2 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

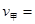 千米/时,
千米/时,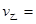 千米/时。(2分)
千米/时。(2分)查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 线路 | 弯路(宁波—杭州—上海) | 直路(宁波—跨海大桥—上海) |
| 路程 | 316公里 | 196公里 |
| 过路费 | 140元 | 180元 |
 升,汽油价格为5.00元/升,问
升,汽油价格为5.00元/升,问 为何值时,走哪条线路的总费用较少(总费用=过路费+油耗费);
为何值时,走哪条线路的总费用较少(总费用=过路费+油耗费);查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com