
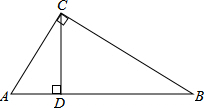
 在△ABC中,∠C=90°,∠B=30°,AC=5$\sqrt{2}$,BC=5$\sqrt{6}$,CD⊥AB于点D.
在△ABC中,∠C=90°,∠B=30°,AC=5$\sqrt{2}$,BC=5$\sqrt{6}$,CD⊥AB于点D.分析 (1)根据CD⊥AB,∠B=30°,可得Rt△BCD中,CD=$\frac{1}{2}$BC;
(2)根据轴对称变换,得到点B'的位置,进而得到△AB′C,根据△ABB'为等腰三角形,即可得到△AB′B的面积.
解答 解:(1)∵CD⊥AB,BC=5$\sqrt{6}$,∠B=30°,
∴Rt△BCD中,CD=$\frac{1}{2}$BC=$\frac{5}{2}\sqrt{6}$;
(2)如图所示,△AB′C即为所求;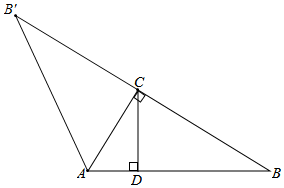
由轴对称的性质可得,B'C=BC=5$\sqrt{6}$,∠BCB'=180°,
∴BB'=10$\sqrt{6}$,
∴△AB′B的面积=$\frac{1}{2}$BB'×AC=$\frac{1}{2}$×10$\sqrt{6}$×5$\sqrt{2}$=50$\sqrt{3}$.
点评 本题主要考查了利用轴对称变换进行作图,含30°角直角三角形的性质以及三角形面积的计算,解题时注意:在直角三角形中,30°角所对的直角边等于斜边的一半.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{16}$=±4 | B. | $\sqrt{(-2)^{2}}$=2 | C. | $\sqrt{27}$=3 | D. | $\frac{1}{\sqrt{3}}$=$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com