

���� ��1��ֻҪ֤����EOC=��OCH���ɵ�OE��CH��EC��OH����֤����
��2��B�������ǣ�0��$\frac{5\sqrt{3}}{3}$�����ı���OECH�����Σ����ȸ��ݶԽ������ֱ��ƽ���ı��������Σ��ж��ı���OECH�����Σ������Ƴ���EOB=��EOC=��ECO=30�㣬�ɴ˼��ɽ�����⣻
��3��������������⼴�ɣ��ٵ���F�ڵ�O��G֮��ʱ����ͼ3���ڵ���G��O��F֮��ʱ����ͼ4��
��� ��1��֤������ͼ1��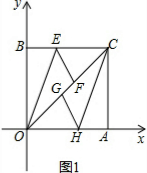
���ı���OBCAΪ���Σ�
��OB��CA��BC��OA��
���BOC=��OCA��
�֡ߡ�BOE����OE���ۣ�ʹ��B����OC�ϵ�F�㴦����ACH����CH���ۣ�ʹ��A����OC�ϵ�G�㴦��
���BOC=2��EOC����OCA=2��OCH��
���EOC=��OCH��
��OE��CH��
�֡�BC��OA��
���ı���OECH��ƽ���ı��Σ�
��2���⣺��B�������ǣ�0��$\frac{5\sqrt{3}}{3}$�����ı���OECH�����Σ��������£���ͼ2��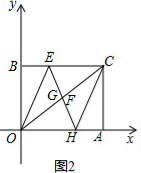
�ߡ�BOE����OE���ۣ�ʹ��B����OC�ϵ�F�㴦����ACH����CH���ۣ�ʹ��A����OC�ϵ�G�㴦��
���EFO=��EBO=90�㣬��CFH=��CAF=90�㣬
�ߵ�F��G�غϣ�
��EH��OC��
�֡��ı���OECH��ƽ���ı��Σ�
��ƽ���ı���OECH�����Σ�
��EO=EC��
���EOC=��ECO��
�֡ߡ�EOC=��BOE��
���EOB=��EOC=��ECO=30�㣬
�֡ߵ�A�������ǣ�5��0����
��OA=5��
��BC=5��
��Rt��OBC��OB=$\frac{\sqrt{3}}{3}$BC=$\frac{5\sqrt{3}}{3}$��
���B�������ǣ�0��$\frac{5\sqrt{3}}{3}$����
��3���⣺�ٵ���F�ڵ�O��G֮��ʱ����ͼ3��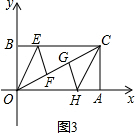
�ߡ�BOE����OE���ۣ�ʹ��B����OC�ϵ�F�㴦����ACH����CH���ۣ�ʹ��A����OC�ϵ�G�㴦��
��OF=OB��CG=CA��
��OB=CA��
��OF=CG��
�ߵ�F��G���Խ���OC���ȷ֣�
��AC=OF=FG=GC��
��AC=m����OC=3m��
��Rt��OAC��OA=5��
��AC2+OA2=OC2��
��m2+52=��3m��2�����m=$\frac{5\sqrt{2}}{4}$��
��OB=AC=$\frac{5\sqrt{2}}{4}$��
���B�������ǣ�0��$\frac{5\sqrt{2}}{4}$����
�ڵ���G��O��F֮��ʱ����ͼ4��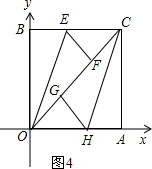
ͬ���ɵ�OF=CG=AC��
��OG=n����AC=GC=2n��
��Rt��OAC��OA=5��
��AC2+OA2=OC2��
�ࣨ2n��2+52=��3n��2�����n=$\sqrt{5}$��
��AC=OB=2 $\sqrt{5}$��
���B�������ǣ�0��2 $\sqrt{5}$����
���� ���⿼�����ı��ε��ۺ��⣺�������վ��ε����ʡ�ƽ���ı��κ����ε��ж��������۵������ʡ����ɶ�����֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ�����÷������۵�˼������ѧ���⣬�����п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a6��a3=a2 | B�� | ��ab3��3=ab6 | C�� | ��a+2��2=a2+4 | D�� | x12��x6=x6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
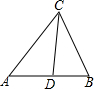 ��ͼ��CD�ǡ�ABC�Ľ�ƽ���ߣ���A=50�㣬��B=60�㣬���ACD�Ķ����ǣ�������
��ͼ��CD�ǡ�ABC�Ľ�ƽ���ߣ���A=50�㣬��B=60�㣬���ACD�Ķ����ǣ�������| A�� | 35�� | B�� | 40�� | C�� | 145�� | D�� | 110�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
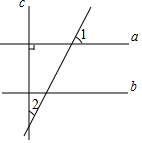 ��ͼ����ֱ֪��a��c��ֱ��b��c������1=65�㣬���2�Ķ���Ϊ��������
��ͼ����ֱ֪��a��c��ֱ��b��c������1=65�㣬���2�Ķ���Ϊ��������| A�� | 20�� | B�� | 25�� | C�� | 50�� | D�� | 65�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪��A��-1��0����B��4��0����������y=ax2+bx-4��x����������㣬��C����������y��Ľ��㣬����AC�������ߵĶԳ�����x�ύ�ڵ�M��
��ͼ����֪��A��-1��0����B��4��0����������y=ax2+bx-4��x����������㣬��C����������y��Ľ��㣬����AC�������ߵĶԳ�����x�ύ�ڵ�M���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
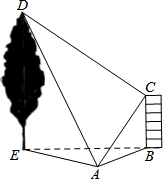 ��ͼ����ˮƽ��������һ������BC��һ����DE���ڵ���۲��A������ݶ�C������D�����Ƿֱ���45����60�㣬��CAD=60�㣬���ݶ�C����á�DCA=90�㣮�����ݵĸ�BC=6�ף�������DE�ij��ȣ�
��ͼ����ˮƽ��������һ������BC��һ����DE���ڵ���۲��A������ݶ�C������D�����Ƿֱ���45����60�㣬��CAD=60�㣬���ݶ�C����á�DCA=90�㣮�����ݵĸ�BC=6�ף�������DE�ij��ȣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a2•a3=a6 | B�� | ��2ab2��2=4a2b4 | C�� | ��-a2��3=a6 | D�� | 2a2��a=2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
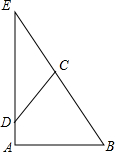 ��ͼ����֪Rt��ABE�С�A=90�㣬��B=60�㣬BE=10��D���߶�AE�ϵ�һ���㣬��D��CD��BE��C����ʹ�á�CDE=30�㣬��CD���ȵ�ȡֵ��Χ��0��CD��5��
��ͼ����֪Rt��ABE�С�A=90�㣬��B=60�㣬BE=10��D���߶�AE�ϵ�һ���㣬��D��CD��BE��C����ʹ�á�CDE=30�㣬��CD���ȵ�ȡֵ��Χ��0��CD��5���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com