
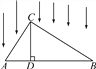
【题目】如图所示,△ABC被平行光线照射,CD⊥AB于D,AB在投影面上.
(1)指出图中AC的投影是什么?CD与BC的投影呢?
(2)探究:当△ABC为直角三角形(∠ACB=90°)时,易得AC2=AD·AB,此时有如下结论:直角三角形一直角边的平方等于它在斜边射影与斜边的乘积,这一结论我们称为射影定理.通过上述结论的推理,请证明以下两个结论.
①BC2=BD·AB;②CD2=AD·BD.
【答案】(1)AC的投影是AD,CD的投影是点D,BC的投影是BD;(2)证明见解析.
【解析】试题分析:(1)在平行投影中,投影线垂直于投影面产生的投影叫做正投影,根据正投影的定义求解即可;
(2)①,结合两角对应相等的两三角形相似,可得△BCD∽△BAC,根据相似三角形对应边成比例可证明结论;
②同理可证△ACD∽△CBD,根据相似三角形对应边成比例可证明结论成立.
试题解析:
解:(1)∵CD⊥AB,
而平行光线垂直AB,
∴AC的投影是AD,CD的投影是点D,BC的投影为BD;
(2)①∵∠ACB=90°,CD⊥AB于D,
∴∠ACB=∠CDB=90°.
∵∠B=∠B,
∴△BCD∽△BAC,
∴![]() ,
,
∴BC2=BDAB;
②同理可得:△ACD∽△CBD,
∴![]() ,
,
∴CD2=ADBD.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:
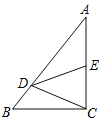
【题目】如图,在Rt△ABC中,∠C=90°,点D在边AB上,线段DC绕点D逆时针旋转,端点C恰巧落在边AC上的点E处.如果![]() ,
,![]()
求m与n满足的关系式(用含n的代数式表示m).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,BC=8cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s).
(1)连接EF,当EF经过AC边的中点D时,求证:△ADE≌△CDF;
(2)①当t为 时,以A、F、C、E为顶点的四边形是平行四边形(直接写出结果);
②当t为 时,四边形ACFE是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
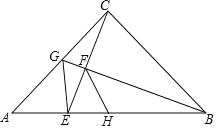
【题目】如图,△ABC中,∠ACB=90°,AC=BC,点G为AC中点,连结BG,CE⊥BG于F,交AB于E,连接GE,点H为AB中点,连接FH.以下结论:(1)∠ACE=∠ABG;(2)∠AGE=∠CGB:(3)若AB=10![]() ,则BF=4
,则BF=4![]() ;(4)FH平分∠BFE;(5)S△BGC=3S△CGE.其中正确结论的个数是( )
;(4)FH平分∠BFE;(5)S△BGC=3S△CGE.其中正确结论的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD的面积为300cm2,长和宽的比为3:2.在此长方形内沿着边的方向能否并排裁出两个面积均为147cm2的圆(π取3),请通过计算说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市举行“行动起来,对抗雾霾”为主题的植树活动,某街道积极响应,决定对该街道进行绿化改造,共购进甲、乙两种树共50棵,已知甲树每棵800元,乙树每棵1200元.
(1)若购买两种树的总金额为56000元,求甲、乙两种树各购买了多少棵?
(2)若购买甲树的金额不少于购买乙树的金额,至少应购买甲树多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠B =∠C,点D、E分别是边AB、AC上的点,PD平分∠BDE交BC于H,PE平分∠DEC交BC于G,DQ平分∠ADE交PE延长线于Q。

(1)∠A+∠B+∠C+∠P +∠Q = °;
(2)猜想∠P与∠A的数量关系,并证明你的猜想;
(3)若∠EGH =112°,求∠ADQ 的大小。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com