
【题目】某中学开展菜市场菜价调查活动,以锻炼同学们的生活能力.调查一共连续7天,每天调查3次,第一次8:00由各班的A小组调查,第二次13:00由B小组调查,第三次17:00由C小组调查.调查完后分析当天的菜价波动情况,七天调查结束后整理数据,就得出了菜价最便宜的某一时段.下面是同学们的一些调查情况,请你帮忙分析数据: 第1天菜价调查情况(单位:元/千克) 第2﹣5天平均菜价(单位:元/千克)
(1)根据“第2﹣5天平均菜价”图来分析:哪种蔬果价格最便宜?
(2)从第一天的调查情况来看,哪种蔬果的价格波动最小?请通过计算说明.
(3)计算苹果、白菜、土豆在1﹣5天的平均菜价.
(4)根据上面两个图来分析:在3﹣5天中的哪一天的哪一时段购买苹果最省钱?
【答案】
(1)解:根据“第2﹣5天平均菜价”图可知,
3元/千克≤苹果的价格≤4元/千克,
4元/千克≤白菜的价格≤5元/千克,
5元/千克≤土豆的价格≤6元/千克,
所以苹果的价格最便宜;
(2)解:根据“第1天菜价调查情况”图可知,
土豆的价格波动范围是:4﹣3=1(元/千克),
白菜的价格波动范围是:5﹣3=2(元/千克),
苹果的价格波动范围是:6﹣4=2(元/千克),
所以土豆的价格波动最小
(3)解:第1天的平均菜价为:
苹果: ![]() (6+5+4)=5(元/千克),白菜:
(6+5+4)=5(元/千克),白菜: ![]() (5+3+4)=4(元/千克),土豆:
(5+3+4)=4(元/千克),土豆: ![]() (4+4+3)=
(4+4+3)= ![]() (元/千克),
(元/千克),
它们在1﹣5天的平均菜价为:
苹果: ![]() (5+3+4+3+4)=
(5+3+4+3+4)= ![]() (元/千克),白菜:
(元/千克),白菜: ![]() (4+4+5+4+5)=
(4+4+5+4+5)= ![]() (元/千克),土豆:
(元/千克),土豆: ![]() (
( ![]() +5+6+5+6)=
+5+6+5+6)= ![]() (元/千克)
(元/千克)
(4)解:根据上面第一个图可知,苹果在17:00以后价格较低,根据第二个图可知,苹果在第二天或第四天价格较低,
所以在3﹣5天中的第四天的17:00购买苹果最省钱.
【解析】(1)根据“第2﹣5天平均菜价”图可知,苹果的价格最便宜;(2)根据“第1天菜价调查情况”图,得出这一天每一种蔬菜的最高价格与最低价格,再用最高价格与最低价格相减比较后即可求出价格波动最小的蔬菜;(3)先分别求出苹果、白菜、土豆第1天的平均菜价,再求出它们在1﹣5天的平均菜价;(4)根据上面第一个图可知,苹果在17:00以后价格较低,根据第二个图可知,苹果在第二天或第四天价格较低,进而得出结论.
【考点精析】解答此题的关键在于理解折线统计图的相关知识,掌握能清楚地反映事物的变化情况,但是不能清楚地表示出在总体中所占的百分比,以及对极差的理解,了解方差的算数平方根叫做这组数据的标准差,用“s”表示.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】下列说法:①倒数等于本身的数是±1;②互为相反数的两个非零数的商为﹣1;③如果两个数的绝对值相等,那么这两个数相等;④有理数可以分为正有理数和负有理数;⑤单项式﹣![]() 的系数是﹣
的系数是﹣![]() ,次数是6;⑥多项式3πa3+4a2﹣8是三次三项式,其中正确的个数是( )
,次数是6;⑥多项式3πa3+4a2﹣8是三次三项式,其中正确的个数是( )
A. 2 个B. 3 个C. 4 个D. 5 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店销售A,B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,销售额为96万元;本周已售2辆A型车和1辆B型车,销售额为62万元.
(1)求每辆A型车和B型车的售价各多少万元.
(2)甲公司拟向该店购买A,B两种型号的新能源汽车共6辆,购车费不少于130万元,且不超过140万元. 则有哪几种购车方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AM∥BN,∠A=60°,点P是射线AM上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
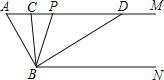
(1)求∠CBD的度数;
(2)当点P运动时,∠APB:∠ADB的比值是否随之变化?若不变,请求出这个比值;若变化,请找出变化规律;
(3)当点P运动到某处时,∠ACB=∠ABD,求此时∠ABC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区在同一线路上顺次有三个景点A,B,C,甲、乙两名游客从景点A出发,甲步行到景点C;乙花20分钟时间排队后乘观光车先到景点B,在B处停留一段时间后,再步行到景点C.甲、乙两人离景点A的路程s(米)关于时间t(分钟)的函数图像如图所示.
(1)甲的速度是 米/分钟;
(2)当20≤t ≤30时,求乙离景点A的路程s与t的函数表达式;
(3)乙出发后多长时间与甲在途中相遇?
(4)若当甲到达景点C时,乙与景点C的路程为360米,则乙从景点B步行到景点C的速度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于点D,过B作BE⊥ED于点E.
求证:△BEC≌△CDA;
(模型应用)
(2)①已知直线l1:y=![]() x+4与坐标轴交于点A、B,将直线l1绕点A逆时针旋转45o至直线l2,如图2,求直线l2的函数表达式;
x+4与坐标轴交于点A、B,将直线l1绕点A逆时针旋转45o至直线l2,如图2,求直线l2的函数表达式;
②如图3,长方形ABCO,O为坐标原点,点B的坐标为(8,-6),点A、C分别在坐标轴上,点P是线段BC上的动点,点D是直线y=-2x+6上的动点且在第四象限.若△APD是以点D为直角顶点的等腰直角三角形,请直接写出点D的坐标.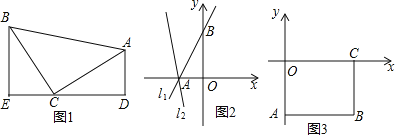
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.
(1)观察猜想
如图1,当点D在线段BC上时,
①BC与CF的位置关系为: .
②BC,CD,CF之间的数量关系为:;(将结论直接写在横线上)
(2)数学思考
如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.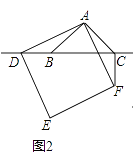
(3)拓展延伸
如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=2 ![]() ,CD=
,CD= ![]() BC,请求出GE的长.
BC,请求出GE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,解决提出的问题:
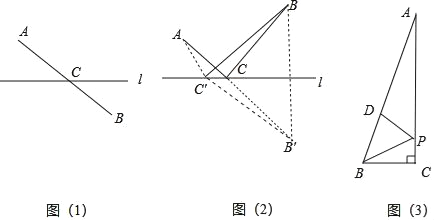
最短路径问题:如图(1),点A,B分别是直线l异侧的两个点,如何在直线l上找到一个点C,使得点C到点A,点B的距离和最短?我们只需连接AB,与直线l相交于一点,可知这个交点即为所求.
如图(2),如果点A,B分别是直线l同侧的两个点,如何在l上找到一个点C,使得这个点到点A、点B的距离和最短?我们可以利用轴对称的性质,作出点B关于的对称点B,这时对于直线l上的任一点C,都保持CB=CB,从而把问题(2)变为问题(1).因此,线段AB与直线l的交点C的位置即为所求.
为了说明点C的位置即为所求,我们不妨在直线上另外任取一点C′,连接AC′,BC′,B′C′.因为AB′≤AC′+C′B′,∴AC+CB<AC'+C′B,即AC+BC最小.
任务:
数学思考
(1)材料中划线部分的依据是 .
(2)材料中解决图(2)所示问题体现的数学思想是 .(填字母代号即可)
A.转化思想
B.分类讨论思想
C.整体思想
迁移应用
(3)如图,在Rt△ABC中,∠C=90°,∠BAC=15°,点P为C边上的动点,点D为AB边上的动点,若AB=8cm,则BP+DP的最小值为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个由若干小正方形堆成的几何体,它从正面看和从左面看的图形如图1所示.
![]() 这个几何体可以是图2中甲,乙,丙中的______;
这个几何体可以是图2中甲,乙,丙中的______;
![]() 这个几何体最多由______个小正方体堆成,最少由______个小正方体堆成;
这个几何体最多由______个小正方体堆成,最少由______个小正方体堆成;
![]() 请在图3中用阴影部分画出符合最少情况时的一个从上面往下看得到的图形.
请在图3中用阴影部分画出符合最少情况时的一个从上面往下看得到的图形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com