
【题目】某商场试销一种成本为每件![]() 元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于
元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于![]() .经试销发现,销售量
.经试销发现,销售量![]() (件)与销售单价
(件)与销售单价![]() (元)符合一次函数关系,当销售单价为
(元)符合一次函数关系,当销售单价为![]() 元时销售量为
元时销售量为![]() 件,当销售单价为
件,当销售单价为![]() 元时销售量为
元时销售量为![]() 件.
件.
(1)此试销期间销售量![]() 可能为
可能为![]() 吗?说明理由.
吗?说明理由.
(2)销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
【答案】(1)不可能,理由见解析;(2)定价75元时,利润最大为1125元.
【解析】
(1)根据一次函数的待定系数法,得到p=-x+120,结合50≤x≤75,即可得到结论;
(2)设销售利润为y元.根据题意得:y=(x-50)(-x+120),结合50≤x≤75与二次函数的性质,即可求解.
(1)不可能.理由如下:
设p=kx+b,
根据题意得:![]() ,解得:
,解得:![]() ,
,
∴p=-x+120,
∴当P=40时,x=80,
又∵50≤x≤75,
∴p不可能是40;
(2)设销售利润为y元.
根据题意得:y=(x-50)(-x+120),
即:y=-x2+170x-6000,
∵x=![]() 且抛物线开口向下,
且抛物线开口向下,
∴50≤x≤75时,y随x的增大而增大,
∴当x=75时,y最大=1125元.
答:销售单价定为75元时,利润最大为1125元.


科目:初中数学 来源: 题型:
【题目】某水果店在两周内,将标价为10元/斤的某种水果,经过两次降价后的价格为8.1元/斤,并且两次降价的百分率相同.
(1)求该种水果每次降价的百分率;
(2)从第一次降价的第1天算起,第x天(x为整数)的售价、销量及储存和损耗费用的相关信息如表所示:
时间x(天) | 1≤x≤7 | 8≤x≤14 |
售价(元/斤) | 第1次降价后的价格 | 第2次降价后的价格 |
销量(斤) | 80﹣3x | 120﹣x |
储存和损耗费用(元) | 40+3x | 3x2﹣64x+400 |
已知该种水果的进价为4.1元/斤,设销售该水果第x(天)的利润为y(元),求y与x(1≤x≤14)之间的函数关系式,并求出第几天时销售利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=4,BC=8,E为CD边的中点,点P、Q为BC边上两个动点,且PQ=2,当BP=_____时,四边形APQE的周长最小.
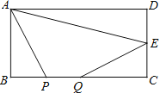
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△AB.C内接于⊙0,点D在半径OB的延长线上,∠BCD=∠A=30°.
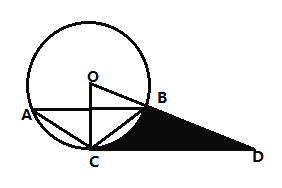
(1)判断直线CD与⊙0的位置关系,并说明理由
(2)若⊙0的半径为1,求阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
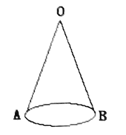
【题目】如图,圆锥母线长![]() 厘米.
厘米.
(1)若底面圆的半径为![]() 厘米,则侧面展开扇形图的圆心角为__________;
厘米,则侧面展开扇形图的圆心角为__________;
(2)若一只蚂蚁从![]() 点出发沿侧面爬行一周回到出发点,最短路径长
点出发沿侧面爬行一周回到出发点,最短路径长![]() 厘米,则侧面展开扇形图的圆心角为__________.
厘米,则侧面展开扇形图的圆心角为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
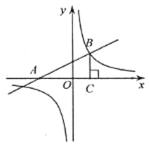
【题目】如图,已知一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与反比例函数
,与反比例函数![]() 的图象的交点为
的图象的交点为![]() ,
,![]() 轴垂足为
轴垂足为![]() ,若点
,若点![]() 在反比例函数图象上,且
在反比例函数图象上,且![]() 的面积等于12,则点
的面积等于12,则点![]() 的坐标为__________.
的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 是圆上不与点
是圆上不与点![]() 重合的动点,连接
重合的动点,连接![]() 并延长到点
并延长到点![]() ,使
,使![]() ,点
,点![]() 是
是![]() 的中点,连接
的中点,连接![]() .
.
(1)求证:![]() ;
;
(2)填空:①若![]() ,当
,当![]() 时,四边形
时,四边形![]() 是菱形;
是菱形;
②当四边形![]() 是正方形时,
是正方形时, ![]() ________°
________°

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习完反比例函数的图象及性质后,老师给冋学们留了这样一道作业题:“已知点(﹣1,m)和点(2,n)都在反比例函数y=![]() (k<0)的图象上,试比较m和n的大小?”以下是彬彬同学的解题过程:
(k<0)的图象上,试比较m和n的大小?”以下是彬彬同学的解题过程:
解:∵在反比例函数y=![]() 中,k<0 ①
中,k<0 ①
∴反比例函数y=![]() ,y随x的增大而增大 ②
,y随x的增大而增大 ②
∵![]() ③
③
∴![]() ④
④
(1)彬彬的解答过程在第 步开始出错,出错的原因是 .请你帮助彬彬写出正确的解答过程.
(2)若点(﹣6,p)、点(1,q)和点(3,z)也在反比例函数y=![]() (k<0)的图象上,直接比较p、q、z的大小 (结果用“<”连结)
(k<0)的图象上,直接比较p、q、z的大小 (结果用“<”连结)
查看答案和解析>>
科目:初中数学 来源: 题型:
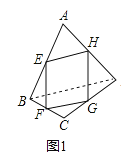
【题目】如图①,已知点E,F,G,H分别是四边形ABCD各边AB,BC,CD,DA的中点,求证四边形FFG是平行四边形.根据以下思路可以证明四边形EFGH是平行四边形:
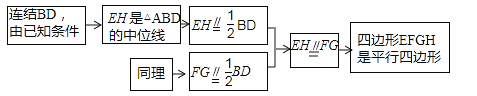
(1)根据上述思路,请你写出完整的证明过程;
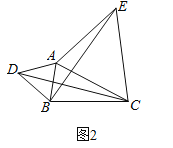
(2)如图,已知![]() ,分别以AB、AC为边,在BC同侧作等边三角形ABD和等边三角形ACE,连接CD,BF.可通过证明△________≌△________,得到
,分别以AB、AC为边,在BC同侧作等边三角形ABD和等边三角形ACE,连接CD,BF.可通过证明△________≌△________,得到![]() ;
;
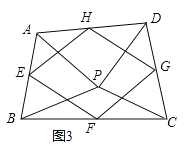
(3)如图③,点P是四边形ABCD内一点,且满足![]() ,
,![]() ,
,![]() ,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想四边形EFGH的形状,并证明.
,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想四边形EFGH的形状,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com