
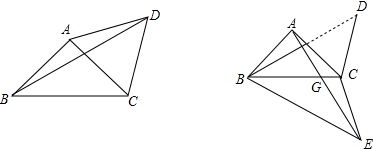
分析 (1)根据等腰直角三角形的性质得到∠ABC=∠ACB=45°,由△ACD是等边三角形,得到∠ACD=∠DAC=∠ADC=60°,于是得到∠BAD=150°,由于AB=AD,于是得到∠ADB=∠ABD=15°,即可得到结论;
(2)根据折叠的性质得到∠BEC=∠BDC=45°,∠BCE=∠BCD=45°+60°=105°,求出∠DBC=∠EBC=30°,证得∠BFG=90°,于是求得FG=$\frac{1}{2}$BG,然后根据等腰三角形的性质得到结论.
解答 解:(1)∵∠CAB=90°,AB=AC,
∴∠ABC=∠ACB=45°,
∵△ACD是等边三角形,
∴∠ACD=∠DAC=∠ADC=60°,
∴∠BAD=150°,
∵AB=AD,
∴∠ADB=∠ABD=15°,
∴∠BDC=45°;
(2) ∵将△BCD沿直线BC折叠得△BCE,
∵将△BCD沿直线BC折叠得△BCE,
∴∠BEC=∠BDC=45°,∠BCE=∠BCD=45°+60°=105°,
∴∠DBC=∠EBC=30°,
∵AC=CD=CE,∠ACE=∠ACB+∠BCE=150°,
∴∠CEG=15°,
∴∠GEB=30°,
∴∠FGB=60°
∴∠BFG=90°,
∴FG=$\frac{1}{2}$BG,
∵∠GBE=∠DBC=∠GEB=30°,
∴BG=GE,
∴GE=2FG=6.
点评 本题考查了翻折变换-折叠问题,等边三角形的性质,等腰直角三角形的性质,熟练掌握各性质定理是解题的关键.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | b>a>c | B. | b>c>a | C. | a>b>c | D. | c>a>b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
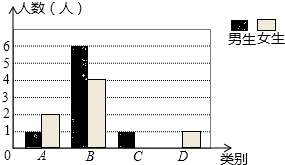 某校七年级共有200名学生,在一次数学测验后,为了解本次测验的成绩情况,从中随机抽取了部分学生的成绩进行统计,并制作了如图表:
某校七年级共有200名学生,在一次数学测验后,为了解本次测验的成绩情况,从中随机抽取了部分学生的成绩进行统计,并制作了如图表:| 等级 | 分数 | 频数 | 频率 |
| A | 90≤x≤100 | 3 | 0.15 |
| B | 80≤x<90 | 10 | a |
| C | 70≤x<80 | b | 0.2 |
| D | 60≤x<70 | c | d |
| 合计 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,在△ABC中,∠A=90°,D为BC的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,试探究线段BE,EF,FC之间的数量关系.
如图所示,在△ABC中,∠A=90°,D为BC的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,试探究线段BE,EF,FC之间的数量关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
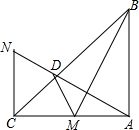 如图,AB⊥AC,NC⊥AC,AB=AC,M为AC中点,AN⊥BM交BC于D,BC平分∠ACN.求证:
如图,AB⊥AC,NC⊥AC,AB=AC,M为AC中点,AN⊥BM交BC于D,BC平分∠ACN.求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
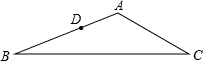 如图,在△ABC中,AB=12cm,BC=18cm,AC=9cm,D为AB上一点,BD=$\frac{2}{3}$AB,E是AC上的一点.若△ADE与△ABC相似,请你画出线段DE并求DE的长.
如图,在△ABC中,AB=12cm,BC=18cm,AC=9cm,D为AB上一点,BD=$\frac{2}{3}$AB,E是AC上的一点.若△ADE与△ABC相似,请你画出线段DE并求DE的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com