
����Ŀ������AOBC�У�OB��8��OA��4���ֱ���OB��OA����ֱ��Ϊx�ᣬy�ᣬ������ͼ1��ʾ��ƽ��ֱ������ϵ��F��BC����һ�����㣨����B��C�غϣ�������F�ķ���������y��![]() ��k��0����ͼ�����AC���ڵ�E��
��k��0����ͼ�����AC���ڵ�E��
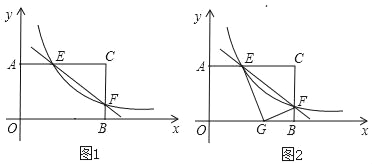
��1������F�˶�����BC���е�ʱ�����E�����ꣻ
��2������EF��AB����֤��EF��AB��
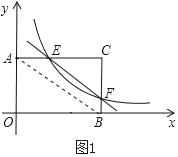
��3����ͼ2������CEF��EF�۵�����Cǡ�����ڱ�OB�ϵĵ�G�������ʱ�����������Ľ���ʽ��
���𰸡���1��E��4��4������2������������3��y��![]()
��������
��1������ȷ����F���꣬�����������������ʽ���ٸ��ݽ���ʽ��õ�E���꼴�ɣ�
��2������AB���ֱ������EFC����ABC������ֵ���ɽ�����⣻
��3���������������жϳ�Rt��MEG��Rt��BGF����ȷ������E��F�������EG��8��![]() ��GF��4��
��GF��4��![]() �����BD������ù��ɶ��������������k���ɵó����ۣ�
�����BD������ù��ɶ��������������k���ɵó����ۣ�
�⣺��1�����ı���OACB�Ǿ��Σ�OB��8��OA��4��
��C��8��4����
�ߵ�F��BC�е㣬
��F��8��2����
�ߵ�F��y��![]() �ϣ�
�ϣ�
��k=16����������������ʽΪy��![]()
�ߵ�E�ڷ���������ͼ���ϣ���E���������Ϊ4��
��4��![]()
��x=4
��E��4��4����
��2������AB�����F��8��a����
��k��8a��
��E��2a��4����
��CF��4��a��EC��8��2a��
��Rt��ECF��tan��EFC��![]() ��2��
��2��
��Rt��ACB��tan��ABC��![]() ��2��
��2��
��tan��EFC��tan��ABC��
���EFC����ABC��
��EF��AB��
��3����ͼ��
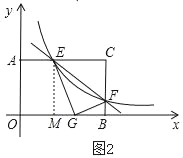
�轫��CEF��EF�۵���Cǡ������OB�ϵ�G�㴦��
���EGF����C��90����EC��EG��CF��GF��
���MGE+��FGB��90����
����E��EM��OB��
���MGE+��MEG��90����
���MEG����FGB��
��Rt��MEG��Rt��BGF��
��![]() ��
��
�ߵ�E��![]() ��4����F��8��
��4����F��8��![]() ����
����
��EC��AC��AE��8��![]() ��CF��BC��BF��4��
��CF��BC��BF��4��![]() ��
��
��EG��EC��8��![]() ��GF��CF��4��
��GF��CF��4��![]() ��
��
��EM��4��
��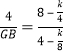 ��
��
��GB��2��
��Rt��GBF��GF2��GB2+BF2��
������4��![]() ��2����2��2+��
��2����2��2+��![]() ��2��
��2��
��k��12��
�෴������������ʽΪy��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
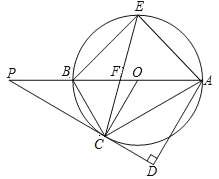
����Ŀ����ͼ��ʾ��AB �ǡ�O ��ֱ����P Ϊ AB �ӳ����ϵ�һ�㣬PC �С�O �ڵ� C��AD��PC�� ����Ϊ D���� CE ƽ�֡�ACB���� AB �ڵ� F������ AE��
��1����֤��PC=PF��
��2���� tan��ABC=![]() ��AE=5
��AE=5![]() �����߶� PC �ij���
�����߶� PC �ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������C�ϲ����������A��B�ײ��ĸ��Ƿֱ�Ϊ30����60�ȣ������ʱ����ĸ߶�CDΪ90�ף��ҵ�A��D��B��ͬһֱ���ϣ�������A��B��ľ��룮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
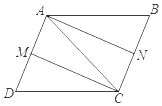
����Ŀ����֪����ͼ����ƽ���ı���ABCD�У�M��N�ֱ���AD��BC���е㣮
��1����֤���ı���AMCN��ƽ���ı��Σ�
��2����AC��CD����֤�ı���AMCN�Ǿ��Σ�
��3������ACD��90�㣬��֤�ı���AMCN�����Σ�
��4����AC��CD����ACD��90�㣬��֤�ı���AMCN�������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
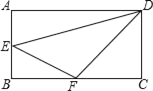
����Ŀ����ͼ���ڳ�����ABCD�У�AB��4cm��BC��8cm��E��F�ֱ���AB��BC���е㣮��E��DF�ľ�����_____cm��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������y=![]() �� y=��kx2+k��k��0����ͬһֱ������ϵ�е�ͼ������ǣ� ������
�� y=��kx2+k��k��0����ͬһֱ������ϵ�е�ͼ������ǣ� ������
A. 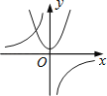 B.
B. 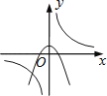 C.
C. 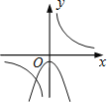 D.
D. 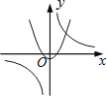
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����һ������Ϊ4Ԫ������Ʒ������ÿ��5Ԫ�ļ۸����ۣ�ÿ��������300��������ÿ��6Ԫ�ļ۸����ۣ�ÿ��������200�����ٶ�ÿ�����ۼ���![]() ��������۸�
��������۸�![]() ��Ԫ/����֮������һ�κ�����ϵ��
��Ԫ/����֮������һ�κ�����ϵ��
��1������![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��2����ÿ�������Ϊ![]() �����
�����![]() ��
��![]() ֮��ĺ�����ϵʽ�������ۼ۸�Ϊ����ʱ������ʹÿ����������ÿ����������Ƕ��٣�
֮��ĺ�����ϵʽ�������ۼ۸�Ϊ����ʱ������ʹÿ����������ÿ����������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪A(��4��a)��B(��1��2)��һ�κ���y1=kx+b�뷴��������y2=![]() (m��0)ͼ����������㣬AC��x����C��
(m��0)ͼ����������㣬AC��x����C��

(1)���k��b��m��ֵ��
(2)����ͼ��ֱ�ӻش��ڵڶ������ڣ���y1��y2ʱ��x��ȡֵ��Χ�� ________��
(3)��P���߶�AB�ϵ�һ�㣬����PC������PCA���������![]() �����P���꣮
�����P���꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����С������ʯͷ����������������Ϸ��ÿһ����Ϸ˫���������������ʯͷ���������������������������Ƶ�һ�֣��涨��ʯͷ��ʤ������������������ʤ��������������ʤ��ʯͷ������ͬ�������Ǻ;֣�
��1��������ͼ���б���������һ����Ϸ�����˻�ʤ�ĸ��ʸ��Ƕ��٣�
��2���������Լ����ֻҪ˭����ʤ���֣��ͳ�����Ϸ��Ӯ�ң�������ͼ���б�����ֻ����������Ϸ����ȷ��Ӯ�ҵĸ��ʣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com