如图所示.是由若干个相同的小正方体搭成的几何体的三视图.该几何体由多少个小正方体搭成6．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

16．

如图所示，是由若干个相同的小正方体搭成的几何体的三视图，该几何体由多少个小正方体搭成6．

分析主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形．

解答解：易得第一层有4个正方体，第二层有2个正方体，共有6个小正方体，
故答案为：6．

点评此题考查学生对三视图掌握程度和灵活运用能力，同时也体现了对空间想象能力方面的考查．如果掌握口诀“俯视图打地基，正视图疯狂盖，左视图拆违章”就更容易得到答案．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：填空题

14．计算$\sqrt{{{（{\frac{1}{4}}）}^2}}$的平方根为±$\frac{1}{2}$．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

15．若△ABC∽△DEF，△ABC与△DEF的相似比为1：2，则它们的周长比为（　　）

A．

1：4

B．

1：2

C．

2：1

D．

1：$\sqrt{2}$

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

4．阅读下列材料：
问题：已知方程x²+x-1=0，求一个一元二次方程，使它的根分别是已知方程根的2倍．
解：设所求方程的根为y，则y=2x，所以x=$\frac{y}{2}$，把x=$\frac{y}{2}$，代入已知方程，得（$\frac{y}{2}$）²+$\frac{y}{2}$-1=0．
化简，得y²+2y-4=0，
故所求方程为y²+2y-4=0
这种利用方程根的代换求新方程的方法，我们称为“换根法”．
请用阅读材料提供的“换根法”求新方程（要求：把所求方程化为一般形式）：
（1）已知方程x²+2x-1=0，求一个一元二次方程，使它的根分别是已知方程根的相反数，则所求方程为y²-2y-1=0；
（2）已知关于x的一元二次方程ax²+bx+c=0（a≠0）有两个不等于零的实数根，求一个一元二次方程，使它的根分别是已知方程根的倒数．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

11．

把四张形状大小完全相同的小长方形卡片（如图①）不重叠的放在一个底面为长方形（长为m厘米，宽为n厘米）的盒子底部（如图②），盒子底面未被卡片覆盖的部分用阴影表示，则图②中两块阴影部分的周长和是（　　）

A．

4n厘米

B．

4m厘米

C．

2（m+n）厘米

D．

4（m+n）厘米

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

1．

如图，在Rt△ABC中，∠C=90°，∠A=60°，AB=12cm，若点P从点B出发以2cm/s的速度向点A运动，点Q从点A出发以1cm/s的速度向点C运动，设P、Q分别从点B、A同时出发，运动的时间为ts．
（1）用含t的式子表示线段AP、AQ的长；
（2）当t为何值时，△APQ是以PQ为底边的等腰三角形？
（3）当t为何值时，PQ∥BC？

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

8．

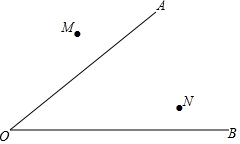2016年6月10日，我海军两艘军舰“温州526舰”、“马鞍山525舰”在我钓鱼岛海域进行巡航．如图，两舰约定在点P会合，已知P点到M、N两地的距离相等，且到OA、OB两条航线的距离相等，请在下图中找出P点的位置．（保留作图痕迹，不写作法）