已知长方形ABCD中,点E在AB边上且AE=BC,F为EB的中点,M为AD边的一个三等分点.
(1)画出相应图形,并求出图中线段的条数;
(2)若图中所有线段的长均为整数,且这些长度之和为39,求长方形ABCD的面积;
(3)若点G、H在边DC上,N在BC上,且BN=AM,DG=AE,CH=BF,分别连接MN、EG、FH.求所得图形中所有长方形的面积的和.
分析:(1)任意两点都可以组成一条线段,所以n条线段可以组成
条线段.
(2)根据题意列出二元一次方程组,再根据求二元一次方程的正整数解解答.
(3)根据图形,把长方形的长和宽分别计算出来,然后计算出所求长方形的面积.
解答: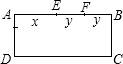
解:(1)∵AB边上共有4个点,
∴
==6,
∴AB边上共有6条线段;
∵AD边上共有3个点,
∴
==3,
∴AB边上共有3条线段,
DC边上共有1条线段,BC边上共有1条线段,
6+3+1+1=11(条),
故共11条线段.
(2)根据题意设AE=BC=x,EF=FB=y,
AB边上共有6条线段,长度和AE+AF+AB+EF+EB+FB=3x+7y,
AD边上共有3条线段,长度和为AM+AD+MD=2x,
BC=x,DC=x+2y,
以上11条线段的长度和为7x+9y,得,
7x+9y=39,
因为所有线段的长均为整数,
解得:x=3,y=2,
ABCD的面积为7×3=21.
(3)所有长的和为3+5+7+2+4+2=23,
所有宽的和1+2+3=6,
所有长方形的面积和为6×23=138.
点评:本题主要考查二元一次方程整数解的求法,数形结合的方法经常是解决一些几何问题的常用方法.

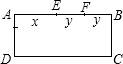 解:(1)∵AB边上共有4个点,
解:(1)∵AB边上共有4个点,

 等?
等?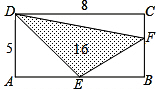 小明在研究直角三角形的边长时,发现了下面的式子:
小明在研究直角三角形的边长时,发现了下面的式子: