
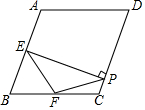
 如图,在菱形ABCD中,∠A=110°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC的度数为( )
如图,在菱形ABCD中,∠A=110°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC的度数为( )| A. | 55° | B. | 50° | C. | 45° | D. | 35° |
分析 首先延长PF交AB的延长线于点G.根据已知可得∠B,∠BEF,∠BFE的度数,再根据余角的性质可得到∠EPF的度数,从而不难求得∠FPC的度数.
解答 解:延长PF交AB的延长线于点G.如图所示:
在△BGF与△CPF中,$\left\{\begin{array}{l}{∠GBF=∠PCF}&{\;}\\{BF=CF}&{\;}\\{∠BFG=∠CFP}&{\;}\end{array}\right.$,
∴△BGF≌△CPF(ASA),
∴GF=PF,
∴F为P G中点.
G中点.
又∵由题可知,∠BEP=90°,
∴EF=$\frac{1}{2}$PG,
∵PF=$\frac{1}{2}$PG,
∴EF=PF,
∴∠FEP=∠EPF,
∵∠BEP=∠EPC=90°,
∴∠BEP-∠FEP=∠EPC-∠EPF,即∠BEF=∠FPC,
∵四边形ABCD为菱形,
∴AB=BC,∠ABC=180°-∠A=70°,
∵E,F分别为AB,BC的中点,
∴BE=BF,∠BEF=∠BFE=$\frac{1}{2}$(180°-70°)=55°,
∴∠FPC=55°;
故选:A.
点评 此题主要考查了菱形的性质以及全等三角形的判定与性质.注意准确作出辅助线是解此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正五边形的边长为2,连接对角线AD、BE、CE,线段AD分别与BE和CE相交于点M、N,给出下列结论:①∠AME=108°,②AN2=AM•AD;③MN=3-$\sqrt{5}$;④S△EBC=2$\sqrt{5}$-1,其中正确的结论是①②③(把你认为正确结论的序号都填上).
如图,正五边形的边长为2,连接对角线AD、BE、CE,线段AD分别与BE和CE相交于点M、N,给出下列结论:①∠AME=108°,②AN2=AM•AD;③MN=3-$\sqrt{5}$;④S△EBC=2$\sqrt{5}$-1,其中正确的结论是①②③(把你认为正确结论的序号都填上).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知抛物线y=-x2+9的顶点为A,曲线DE是双曲线y=$\frac{k}{x}$(3≤x≤12)的一部分,记作G1,且D(3,m)、E(12,m-3),将抛物线y=-x2+9水平向右移动a个单位,得到抛物线G2.
如图,已知抛物线y=-x2+9的顶点为A,曲线DE是双曲线y=$\frac{k}{x}$(3≤x≤12)的一部分,记作G1,且D(3,m)、E(12,m-3),将抛物线y=-x2+9水平向右移动a个单位,得到抛物线G2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解一批日光灯的使用寿命适宜采用抽样调查 | |
| B. | “打开电视,正在播放《沈视早报》”是必然事件 | |
| C. | 数据1,1,2,2,3的众数是3 | |
| D. | 一组数据的波动越大,方差越小 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com