
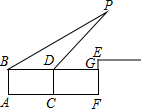
 某学校组织数学兴趣小组的学生,进行一次课外数学实践探究活动,活动课题:利用直角三角形的边角关系,测量“底部不可以到达的旗杆高度”,活动的方式:两个人一个小组,测量后全班交流研讨,活动工具:测倾器,长度相同的标杆若干,皮尺等测量工具,已知领操台EM距地面的高EF为2m,标杆的长为1.6m,甲乙两人分在一组,测量步骤如下:
某学校组织数学兴趣小组的学生,进行一次课外数学实践探究活动,活动课题:利用直角三角形的边角关系,测量“底部不可以到达的旗杆高度”,活动的方式:两个人一个小组,测量后全班交流研讨,活动工具:测倾器,长度相同的标杆若干,皮尺等测量工具,已知领操台EM距地面的高EF为2m,标杆的长为1.6m,甲乙两人分在一组,测量步骤如下:分析 如图,延长BD交EF于G,交PM的延长线于H.则四边形ABDC是矩形,四边形ABGF是矩形,四边形EMHG是矩形,设PD=DH=x,在Rt△PBH中,根据tan30°=$\frac{PH}{BH}$,列出方程即可解决问题.
解答 解:如图作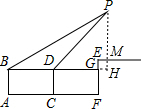 延长BD交EF于G,交PM的延长线于H.则四边形ABDC是矩形,四边形ABGF是矩形,四边形EMHG是矩形,
延长BD交EF于G,交PM的延长线于H.则四边形ABDC是矩形,四边形ABGF是矩形,四边形EMHG是矩形,
∴BD=AC=12m,AB=CD=GF=1.6m,EF=2m,EG=HM=0.4m
在Rt△PDH中,∵∠PDH=45°,
∴PH=DH,设PD=DH=x,
在Rt△PBH中,∵tan30°=$\frac{PH}{BH}$,
∴$\frac{\sqrt{3}}{3}$=$\frac{x}{x+12}$,
解得x=6$\sqrt{3}$+6≈16.39,
∴PM=PH-HM=16.39-0.4≈16.0m.
答:旗杆PM的高度为16.0m.
点评 本题考查解直角三角形的应用-仰角俯角问题、锐角三角函数、矩形的性质等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,学会用构建方程的思想思考问题.


科目:初中数学 来源: 题型:解答题
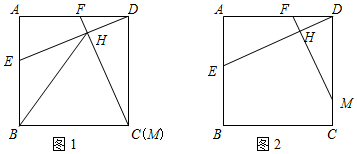
 如图,已知矩形ABCD(AB<AD).
如图,已知矩形ABCD(AB<AD).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
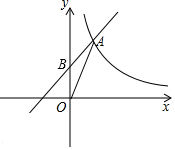 如图,一次函数y=x+$\frac{3}{2}$的图象反比例函数y=$\frac{k}{x}$的图象在第一象限的一个交点为A(1,m),与y轴交于B点.
如图,一次函数y=x+$\frac{3}{2}$的图象反比例函数y=$\frac{k}{x}$的图象在第一象限的一个交点为A(1,m),与y轴交于B点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com