练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知抛物线经过（0,-1）,（3,2）两点．求它的解析式及顶点坐标．

    抛物线的解析式为；抛物线的顶点坐标为（1,-2）．.

    解析试题分析：根据抛物线经过（0,-1）,（3,2）两点,求出 的值,从而得到抛物线解析式,再化成顶点式,求出顶点坐标.
    解：∵抛物线过（0,-1）,（3,2）两点,
    ∴
    解得,  
    ∴抛物线的解析式为．
    ∵,
    ∴抛物线的顶点坐标为（1,-2）．
    考点：抛物线.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    如图，在平面直角坐标系xOy中，A、B为x轴上两点，C、D为y轴上两点，经过A、C、B的抛物线的一部分与经过点A、D、B的抛物线的一部分组合成一条封闭曲线，我们把这条封闭曲线称为“蛋线”．已知点C的坐标为（0，），点M是抛物线：的顶点．

    （1）求A、B两点的坐标．
    （2）“蛋线”在第四象限上是否存在一点P，使得的面积最大？若存在，求出面积的最大值；若不存在，请说明理由；
    （3）当为直角三角形时，直接写出m的值．______

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    今年,在端午节前夕,三位同学到某超市调研一种进价为2元的粽子的销售情况．（售价不低于进价）.请根据小丽提供的信息,解答小华和小明提出的问题．

    认真阅读上面三位同学的对话,请根据小丽提供的信息．
    （1）解答小华的问题；
    （2）解答小明的问题．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    一家化工厂原来每月利润为120万元，从今年1月起安装使用回收净化设备(安装时间不计)，一方面改善了环境，另一方面大大降低原料成本．据测算，使用回收净化设备后的1至x月(1≤x≤12)的利润的月平均值w(万元)满足w＝10x＋90，第二年的月利润稳定在第1年的第12个月的水平．
    (1)设使用回收净化设备后的1至x月(1≤x≤12)的利润和为y，写出y关于x的函数关系式，并求前几个月的利润和等于700万元；
    (2)当x为何值时，使用回收净化设备后的1至x月的利润和与不安装回收净化设备时x个月的利润和相等；
    (3)求使用回收净化设备后两年的利润总和．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    已知：抛物线与x轴的两个交点分别为A（1，0）和B（3，0），与y轴交于点C.

    （1）求此二次函数的解析式；
    （2）写出点C的坐标________，顶点D的坐标为__________；
    （3）将直线CD沿y轴向下平移3个单位长度，求平移后直线m的解析式；
    （4）在直线m上是否存在一点E，使得以点E、A、B、C为顶点的四边形是梯形，如果存在，请直接写出所有满足条件的E点的坐标__________________________________（不必写出过程）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    已知抛物线与x轴相交于两点A(1，0)，B(-3，0)，与y轴相交于点C(0，3)．
    (1)求此抛物线的函数表达式；
    (2)如果点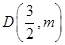是抛物线上的一点，求△ABD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，已知二次函数y=x2+bx+c过点A（1，0），C（0，﹣3）．

    （1）求此二次函数的解析式；
    （2）在抛物线上存在一点P使△ABP的面积为10，请求出出点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，已知抛物线经过A（﹣3，0），B（1，0）两点，与y轴交于点C，其顶点为D，对称轴是直线l，l与x轴交于点H．

    （1）求该抛物线的解析式；
    （2）若点P是该抛物线对称轴l上的一个动点，求△PBC周长的最小值；
    （3）若E是线段AD上的一个动点（ E与A、D不重合），过E点作平行于y轴的直线交抛物线于点F，交x轴于点G，设点E的横坐标为m，△ADF的面积为S．
    ①求S与m的函数关系式；
    ②S是否存在最大值？若存在，求出最大值及此时点E的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，在矩形OABC中，点A（0，10），C（8，0）.沿直线CD折叠矩形OABC的一边BC，使点B落在OA边上的点E处．分别以OC， OA所在的直线为x轴，y轴建立平面直角坐标系，抛物线经过O，D，C三点．

    （1）求D的的坐标及抛物线的解析式；
    （2）一动点P从点E出发，沿EC以每秒2个单位长的速度向点C运动，同时动点Q从点C出发，沿CO以每秒1个单位长的速度向点O运动，当点P运动到点C时，两点同时停止运动．设运动时间为t秒，当t为何值时，以P、Q、C为顶点的三角形与△ADE相似？
    （3）点N在抛物线对称轴上，点M在抛物线上，是否存在这样的点M与点N，使以M，N，C，E为顶点的四边形是平行四边形？若存在，请直接写出点M与点N的坐标（不写求解过程）；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案