
【题目】已知,△ABC中,AC=BC,∠ACB=90°,D为AB的中点,若E在直线AC上任意一点,DF⊥DE,交直线BC于F点.G为EF的中点,延长CG交AB于点H.

(1)若E在边AC上.
①试说明DE=DF;
②试说明CG=GH;
(2)若AE=3,CH=5.求边AC的长.
【答案】(1)①证明见解析;②证明见解析;(2)AC=7或1.
【解析】
试题分析:(1)①连接CD,推出CD=AD,∠CDF=∠ADE,∠A=∠DCB,证△ADE≌△CDF即可;②连接DG,根据直角三角形斜边上中线求出CG=EG=GF=DG,推出∠GCD=∠GDC,推出∠GDH=∠GHD,推出DG=GH即可;
(2)求出EF=5,根据勾股定理求出EC,即可得出答案.
试题解析:(1)①连接CD,∵∠ACB=90°,D为AB的中点,AC=BC,∴CD=AD=BD,又∵AC=BC,∴CD⊥AB,∴∠EDA+∠EDC=90°,∠DCF=∠DAE=45°,∵DF⊥DE,∴∠EDF=∠EDC+∠CDF=90°,∴∠ADE=∠CDF,在△ADE和△CDF中,∵∠A=∠DCF,AD=CD,∠ADE=∠CDF,∴△ADE≌△CDF,∴DE=DF;
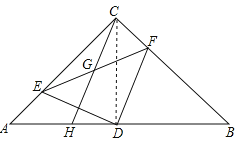
②连接DG,∵∠ACB=90°,G为EF的中点,∴CG=EG=FG,∵∠EDF=90°,G为EF的中点,∴DG=EG=FG,∴CG=DG,∴∠GCD=∠CDG.又∵CD⊥AB,∴∠CDH=90°,∴∠GHD+∠GCD=90°,∠HDG+∠GDC=90°,∴∠GHD=∠HDG,∴GH=GD,∴CG=GH;
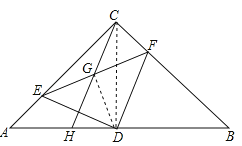
(2)如图,当E在线段AC上时,∵CG=GH=EG=GF,∴CH=EF=5,∵△ADE≌△CDF,∴AE=CF=3,∴在Rt△ECF中,由勾股定理得:CE=![]() =4,∴AC=AE+EC=3+4=7;
=4,∴AC=AE+EC=3+4=7;
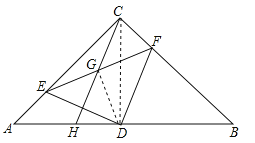
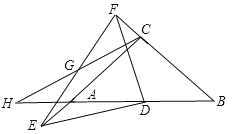
如图,当E在线段CA延长线时,AC=EC﹣AE=4﹣3=1,综合上述:AC=7或1.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】电子跳蚤游戏盘是如图所示的△ABC,AB=8,AC=9,BC=10,如果跳蚤开始时在BC边的点P0处, BP0=4.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3=BP2;跳蚤按上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2015与A间的距离为( )

A.3 B.4 C.5 D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,按如下步骤作图:
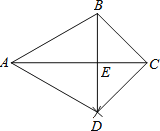
①以A为圆心,AB长为半径画弧;
②以C为圆心,CB长为半径画弧,两弧相交于点D;
③连接BD,与AC交于点E,连接AD,CD.
(1)求证:△ABC≌△ADC;
(2)若∠BAC=30°,∠BCA=45°,AC=4,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区截止到今年栽有果树2400棵,计划今后每年栽果树300棵,x年后,总共栽有果树y棵,则y与x之间的关系式为__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,电线杆上有一盏路灯O,电线杆与三个等高的标杆整齐划一地排列在马路的一侧,AB、CD、EF是三个标杆,相邻的两个标杆之间的距离都是2 m,已知AB、CD在灯光下的影长分别为BM=1.6 m,DN=0.6m.
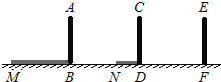
(1)请画出路灯O的位置和标杆EF在路灯灯光下的影子;
(2)求标杆EF的影长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com