练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
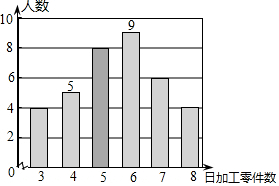
    10．下面的条形图（如图）描述了某车间工人日加工零件的情况，则这些工人日加工零件数的中位数是（　　）
    A．6.5B．6C．5.5D．5

    分析 从条形统计图中找出每天加工零件的数目，进而求出中位数即可．

    解答 解：根据题意得：4，5，8，9，6，4，
    按照从小到大顺序排列为：4，4，5，6，8，9，
    则中位数为$\frac{1}{2}$×（5+6）=5.5，
    故选C

    点评 此题考查了条形统计图，以及中位数，弄清中位数的求法是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    20．计算：（1）（1+3x）（1-3x）=1-9x2，（2）（2x-y）2=4x2-4xy+y2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．计算：
    （1）2$\sqrt{12}$-6$\sqrt{\frac{1}{3}}$+3$\sqrt{48}$
    （2）（2$\sqrt{3}$-3$\sqrt{2}$）2-（$\sqrt{6}$-$\sqrt{5}$）（$\sqrt{6}$+$\sqrt{5}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

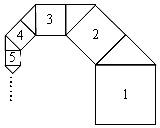    18．如图，第1个正方形（设边长为2）的边为第一个等腰直角三角形的斜边，第一个等腰直角三角形的直角边是第2个正方形的边，第2个正方形的边是第2个等腰三角形的斜边…依此不断连接下去．通过观察与研究，写出第2016个正方形的边长a2016为（　　）
    A．a2016=4（$\frac{1}{2}$）2015B．a2016=2（$\frac{\sqrt{2}}{3}$）2015C．a2016=4（$\frac{1}{2}$）2016D．a2016=2（$\frac{\sqrt{2}}{2}$）2016

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

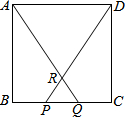    5．如图，正方形ABCD中，P，Q是BC边上的三等分点，连接AQ、DP交于点R．若正方形ABCD的面积为144cm2，则△PQR的面积为6cm2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

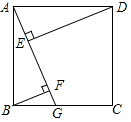    15．如图，G是正方形ABCD边BC上一动点（不与B、C重合）．DE⊥AG于E，BF⊥AG于F，试探究线段DE、EF、BF之间满足怎样的数量关系，写出你的结论，并写出证明过程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．如图，AB∥CD，EF⊥AB于E，已知∠1=35°，则∠2=55°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．新定义函数：在y关于x的函数中，若0≤x≤1时，函数y有最大值和最小值，分别记ymax和ymin，且满足$\left\{\begin{array}{l}{{y}_{min}＞0}\\{2{y}_{min}＞{y}_{max}}\end{array}\right.$，则我们称函数y为“三角形函数”．
    （1）若函数y=x+a为“三角形函数”，求a的取值范围；
    （2）判断函数y=x2-$\frac{\sqrt{2}}{2}$x+1是否为“三角形函数”，并说明理由；
    （3）已知函数y=x2-2mx+1，若对于0≤x≤1上的任意三个实数a，b，c所对应的三个函数值都能构成一个三角形的三边长，则求满足条件的m的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．三个不等于零的有理数a，b，c满足（a+b）（b+c）（c+a）=0，则$\frac{（a+b+c）（{a}^{3}+{b}^{3}+{c}^{3}）（{a}^{5}+{b}^{5}+{c}^{5}）（{a}^{7}+{b}^{7}+{c}^{7}）（{a}^{9}+{b}^{9}+{c}^{9}）}{{a}^{25}+{b}^{25}+{c}^{25}}$=1．

    查看答案和解析>>

    同步练习册答案