
【题目】已知![]() 表示5与-2之差的绝对值,实际上也可理解为5与-2两数在数轴上所对应的两点之间的距离请试着探索:
表示5与-2之差的绝对值,实际上也可理解为5与-2两数在数轴上所对应的两点之间的距离请试着探索:
(1)找出所有符合条件的整数![]() ,使
,使![]() ,这样的整数是__________;
,这样的整数是__________;
(2)利用数轴找出,当![]() 时,
时,![]() 的值是__________;
的值是__________;
(3)利用数轴找出,当![]() 取最小值时,
取最小值时,![]() 的范围是__________.
的范围是__________.
【答案】(1)-4,-3,-2,-1,0,1,2;(2)-5或4;(3)![]() .
.
【解析】
(1)根据绝对值的几何意义,得![]() 表示x与-4两数在数轴上所对应的两点之间的距离,
表示x与-4两数在数轴上所对应的两点之间的距离,![]() 表示x与2两数在数轴上所对应的两点之间的距离,结合条件,即可求解;
表示x与2两数在数轴上所对应的两点之间的距离,结合条件,即可求解;
(2)根据绝对值的几何意义,得![]() 表示x与-3两数在数轴上所对应的两点之间的距离,
表示x与-3两数在数轴上所对应的两点之间的距离,![]() 表示x与2两数在数轴上所对应的两点之间的距离,结合条件,即可求解;
表示x与2两数在数轴上所对应的两点之间的距离,结合条件,即可求解;
(3)根据绝对值的几何意义,得![]() 表示x与-7两数在数轴上所对应的两点之间的距离,
表示x与-7两数在数轴上所对应的两点之间的距离,![]() 表示x与4两数在数轴上所对应的两点之间的距离,结合条件,即可求解.
表示x与4两数在数轴上所对应的两点之间的距离,结合条件,即可求解.
(1)∵![]() =
=![]() 表示x与-4两数在数轴上所对应的两点之间的距离,
表示x与-4两数在数轴上所对应的两点之间的距离,![]() 表示x与2两数在数轴上所对应的两点之间的距离,
表示x与2两数在数轴上所对应的两点之间的距离,
又∵表示2与-4两数在数轴上所对应的两点之间的距离为6,
∴当数轴上表示x的点在表示-4的点的左侧时,![]() ,不符合题意,
,不符合题意,
当数轴上表示x的点在表示2的点的右侧时,![]() ,不符合题意,
,不符合题意,
当数轴上表示x的点在表示-4的点与表示2的点之间(包括表示-4与2的点)时,![]() ,符合题意,
,符合题意,
∴![]() ,
,
∴使![]() ,整数是-4,-3,-2,-1,0,1,2.
,整数是-4,-3,-2,-1,0,1,2.
故答案是:-4,-3,-2,-1,0,1,2;
(2)∵![]() =
=![]() 表示x与-3两数在数轴上所对应的两点之间的距离,
表示x与-3两数在数轴上所对应的两点之间的距离,![]() 表示x与2两数在数轴上所对应的两点之间的距离,
表示x与2两数在数轴上所对应的两点之间的距离,
∴当x=-5时,表示-5与-3两数在数轴上所对应的两点之间的距离为2,表示-5与2两数在数轴上所对应的两点之间的距离为7,即:![]() ,
,
∴x=-5符合题意,
当x=4时,表示4与-3两数在数轴上所对应的两点之间的距离为7,表示4与2两数在数轴上所对应的两点之间的距离为2,即:![]() ,
,
∴x=4符合题意,
综上所述:当![]() 时,
时,![]() 的值是:-5或4.
的值是:-5或4.
故答案是:-5或4;
(3)∵![]() =
=![]() 表示x与-7两数在数轴上所对应的两点之间的距离,
表示x与-7两数在数轴上所对应的两点之间的距离,![]() 表示x与4两数在数轴上所对应的两点之间的距离,
表示x与4两数在数轴上所对应的两点之间的距离,
∴当数轴上表示x的点在表示-7的点的左侧时,![]() ,
,
当数轴上表示x的点在表示4的点的右侧时,![]() ,
,
当数轴上表示x的点在表示-7的点与表示4的点之间(包括表示-7与4的点)时,![]() ,
,
∴当![]() 取最小值时,
取最小值时,![]() .
.
故答案是:![]() .
.


科目:初中数学 来源: 题型:
【题目】已知关于x,y的方程组![]() 给出以下结论:①当a=3时,方程组的解也是方程2x-y=a+13的解;②无论a取何值,x,y的值都不可能互为相反数;③x,y的自然数的解有2对;④若z=
给出以下结论:①当a=3时,方程组的解也是方程2x-y=a+13的解;②无论a取何值,x,y的值都不可能互为相反数;③x,y的自然数的解有2对;④若z=![]() (x+3)y,则z的最大值是36.其中正确的是______.(填序号)
(x+3)y,则z的最大值是36.其中正确的是______.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春暖花开,市民纷纷外出踏青,某种品牌鞋专卖店抓住机遇,利用10周年店庆对其中畅销的M款运动鞋进行促销,M款运动鞋每双的成本价为800元,标价为1200元.
(1)M款运动鞋每双最多降价多少元,才能使利润率不低于20%;
(2)该店以前每周共售出M款运动鞋100双,2017年3月的一个周末,恰好是该店的10周年店庆,这个周末M款运动鞋每双在标价的基础上降价 ![]() m%,结果这个周末卖出的M款运动鞋的数量比原来一周卖出的M款运动鞋的数量增加了
m%,结果这个周末卖出的M款运动鞋的数量比原来一周卖出的M款运动鞋的数量增加了 ![]() m%,这周周末的利润达到了40000元,求m的值.
m%,这周周末的利润达到了40000元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲,乙两名选手参加长跑比赛,乙从起点出发匀速跑到终点,甲先快后慢,半个小时后找到适合自己的速度,匀速跑到终点,他们所跑的路程y(单位:km)随时间x(单位:h)变化的图象,如图所示,则下列结论错误的是( )
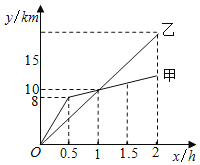
A. 在起跑后1h内,甲在乙的前面
B. 跑到1h时甲乙的路程都为10km
C. 甲在第1.5时的路程为11km
D. 乙在第2h时的路程为20km
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有4个分别标有数字-1,-2,3,4的小球,它们的形状、大小完全相同.小红先从口袋中随机摸出一个小球记下数字为x;小颖在剩下的3个小球中随机摸出一个小球记下数字为y.
(1)小红摸出标有数字3的小球的概率是________;
(2)请用列表或画树状图的方法表示出由x,y确定的点P(x,y)所有可能的结果;
(3)若规定:点P(x,y)在第一象限或第三象限小红获胜,点P(x,y)在第二象限或第四象限小颖获胜,请分别求出两人获胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着通讯技术迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:

(1)这次统计共抽查了 名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为 ;
(2)将条形统计图补充完整;
(3)该校共有1500名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名?
(4)某天甲、乙两名同学都想从“微信”、“QQ”、“电话”三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选中同一种沟通方式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
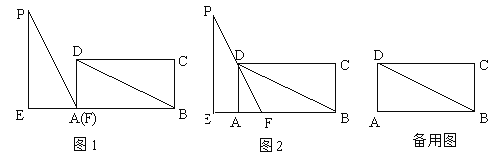
【题目】如图1,在矩形ABCD中,DB=6,AD=3,在Rt△PEF中,∠PEF=90°,EF=3,PF=6,△PEF(点F和点A重合)的边EF和矩形的边AB在同一直线上.现将Rt△PEF从A以每秒1个单位的速度向射线AB方向匀速平移,当点F与点B重合时停止运动,设运动时间为t秒,
解答下列问题:
(1)如图1,连接PD,填空:∠PFD= ,四边形PEAD的面积是 ;
(2)如图2,当PF经过点D时,求 △PEF运动时间t的值;
(3)在运动的过程中,设△PEF与△ABD重叠部分面积为S,请求出S与t的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
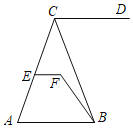
【题目】如图,EF∥AB,∠DCB=65°,∠CBF=15°,∠EFB=130°.
(1)直线CD与AB平行吗?为什么?
(2)若∠CEF=68°,求∠ACB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将证明过程填写完整.
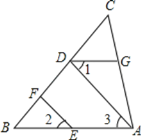
如图,AD⊥BC于点D,EF⊥BC于点F,∠1=∠2.求证AB∥DG.
证明:∵EF⊥BC于点F,AD⊥BC于点D,(已知)
∴∠CFE=∠CDA=90°(___________________________)
∴AD∥ (______________________________________)
∴∠2=∠3(______________________________________)
又∵∠1=∠2(已知)
∴∠1=∠3(________________________)
∴AB∥DG(___________________)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com