
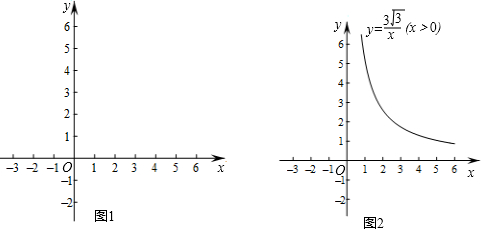
分析 (1)如图1-1中,设点A的“相关直线”交x轴于C或C′,求出C、C′的坐标利用待定系数法即可解决问题;
(2)如图1-2中,由点B的坐标为(0,$\sqrt{3}$),可得点B的“相关直线”为y=$\sqrt{3}$x+$\sqrt{3}$或y=-$\sqrt{3}$x+$\sqrt{3}$,求出y=2$\sqrt{3}$时的自变量的值即可解决问题;
(3)如图2中,当点N的“相关直线”与⊙O相切时,易知直线MN的解析式为y=$\sqrt{3}$x+2$\sqrt{3}$,直线M′N′的解析式为y=$\sqrt{3}$x-2$\sqrt{3}$,求出M、M′的坐标即可解决问题;
解答 解:(1)如图1-1中,设点A的“相关直线”交x轴于C或C′,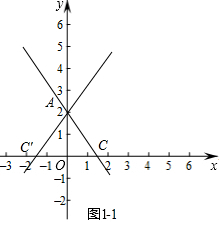
在Rt△AOC中,OA=2,∠ACO=60°,
∴C($\frac{2\sqrt{3}}{3}$,0),同理可得C′(-$\frac{2\sqrt{3}}{3}$,0),
设直线AC的解析式为y=kx+b,则有$\left\{\begin{array}{l}{b=2}\\{\frac{2\sqrt{3}}{3}k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\sqrt{3}}\\{b=2}\end{array}\right.$,
∴直线AC的解析式为y=-$\sqrt{3}$x+2,同法可得直线AC′的解析式为y=$\sqrt{3}$x+2.
(2)如图1-2中,∵若点B的坐标为(0,$\sqrt{3}$),
∴点B的“相关直线”为y=$\sqrt{3}$x+$\sqrt{3}$或y=-$\sqrt{3}$x+$\sqrt{3}$,
∴点B的“相关直线”与直线y=2$\sqrt{3}$交于点C,
点C的坐标为(1,2$\sqrt{3}$)或(-1,2$\sqrt{3}$).
(3)如图2中,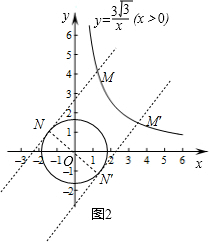
当点N的“相关直线”与⊙O相切时,易知直线MN的解析式为y=$\sqrt{3}$x+2$\sqrt{3}$,直线M′N′的解析式为y=$\sqrt{3}$x-2$\sqrt{3}$,
由$\left\{\begin{array}{l}{y=\sqrt{3}x+2\sqrt{3}}\\{y=\frac{3\sqrt{3}}{x}}\end{array}\right.$可得M(1,3$\sqrt{3}$),
由$\left\{\begin{array}{l}{y=\sqrt{3}x-2\sqrt{3}}\\{y=\frac{3\sqrt{3}}{x}}\end{array}\right.$可得M′(3,$\sqrt{3}$),
观察图象可知,满足条件的点M的横坐标的取值范围1$≤\\;x≤$x≤3.
点评 本题考查反比例函数综合题、一次函数的应用、直角三角形的30度角的性质、点P的“相关直线”的定义等知识,解题的关键是学会用分类讨论的思想思考问题,学会构建一次函数,利用方程组确定函数的交点坐标,属于中考压轴题.


科目:初中数学 来源: 题型:填空题
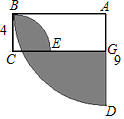 以A为圆心,半径为9的四分之一圆,与以C为圆心,半径为4的四分之一圆如图所示放置,且∠ABC=90°,则图中阴影部分的面积为$\frac{97}{4}$π-36.
以A为圆心,半径为9的四分之一圆,与以C为圆心,半径为4的四分之一圆如图所示放置,且∠ABC=90°,则图中阴影部分的面积为$\frac{97}{4}$π-36.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
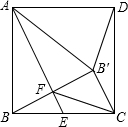 在正方形ABCD中,点E为BC边的中点,把△ABE沿直线AE折叠,B点落在点B′处,B′B与AE交于点F,连接AB′,DB′,FC.下列结论:①AB′=AD;②△FCB′为等腰直角三角形;③∠CB′D=135°;④BB′=BC;⑤AB2=AE•AF.其中正确的个数为( )
在正方形ABCD中,点E为BC边的中点,把△ABE沿直线AE折叠,B点落在点B′处,B′B与AE交于点F,连接AB′,DB′,FC.下列结论:①AB′=AD;②△FCB′为等腰直角三角形;③∠CB′D=135°;④BB′=BC;⑤AB2=AE•AF.其中正确的个数为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
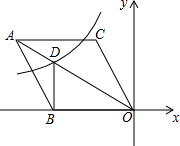 如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,顶点C的坐标为(-$\sqrt{3}$,3),反比例函数y=$\frac{k}{x}$的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,顶点C的坐标为(-$\sqrt{3}$,3),反比例函数y=$\frac{k}{x}$的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )| A. | 4$\sqrt{3}$ | B. | -4$\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | -2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
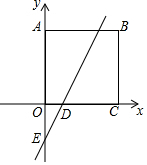 如图,矩形ABCD的顶点B坐标为(5,4),直线y=2x-3分别交x轴、y轴于D、E点,若线段BC上有一点P,直线DE上有一点Q,△APQ是以AP为斜边的等腰直角三角形,则点P坐标为(5,1)或(5,3).
如图,矩形ABCD的顶点B坐标为(5,4),直线y=2x-3分别交x轴、y轴于D、E点,若线段BC上有一点P,直线DE上有一点Q,△APQ是以AP为斜边的等腰直角三角形,则点P坐标为(5,1)或(5,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某商家为了给新产品作宜传,向全社会征集广告用语及商标图案,结果如图所示的商标(图中阴影部分)中标,求此商标图案的面积.(虚线左边为扇形,右边为长方形)
某商家为了给新产品作宜传,向全社会征集广告用语及商标图案,结果如图所示的商标(图中阴影部分)中标,求此商标图案的面积.(虚线左边为扇形,右边为长方形)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com