
【题目】如图,在ABCD中,点E是BC边的中点,连接AE并延长与DC的延长线交于F.

(1)求证:CF=CD;
(2)若AF平分∠BAD,连接DE,试判断DE与AF的位置关系,并说明理由.
【答案】(1)见解析;(2)DE⊥AF
【解析】
试题分析:(1)根据平行四边形的性质可得到AB∥CD,从而可得到AB∥DF,根据平行线的性质可得到两组角相等,已知点E是BC的中点,从而可根据AAS来判定△BAE≌△CFE,根据全等三角形的对应边相等可证得AB=CF,进而得出CF=CD;
(2)利用全等三角形的判定与性质得出AE=EF,再利用角平分线的性质以及等角对等边求出DA=DF,利用等腰三角形的性质求出即可.
(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∵点F为DC的延长线上的一点,
∴AB∥DF,
∴∠BAE=∠CFE,∠ECF=∠EBA,
∵E为BC中点,
∴BE=CE,
则在△BAE和△CFE中,
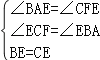 ,
,
∴△BAE≌△CFE(AAS),
∴AB=CF,
∴CF=CD;
(2)解:DE⊥AF,
理由:∵AF平分∠BAD,
∴∠BAF=∠DAF,
∵∠BAF=∠F,
∴∠DAF=∠F,
∴DA=DF,
又由(1)知△BAE≌△CFE,
∴AE=EF,
∴DE⊥AF.


科目:初中数学 来源: 题型:
【题目】闽北某村原有林地120公顷,旱地60公顷,为适应产业结构调整,需把一部分旱地改造为林地,改造后,旱地面积占林地面积的20%,设把x公顷旱地改造为林地,则可列方程为( )
A.60﹣x=20%(120+x) B.60+x=20%×120
C.180﹣x=20%(60+x) D.60﹣x=20%×120
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读题:各类方程的解法不尽相同,但是它们有一个共同的基本数学思想一一转化,把未知转化为已知.无理方程(根号下含有未知数的方程)![]() =2,可以通过方程两边平方把它转化为x+1=4,可得x=3.通过“方程两边平方”解方程,有可能产生增根,必须对解得的根进行检验.例如,把方程
=2,可以通过方程两边平方把它转化为x+1=4,可得x=3.通过“方程两边平方”解方程,有可能产生增根,必须对解得的根进行检验.例如,把方程![]() =x两边平方,得2x+3=x2,解得x1=3,x2=﹣1.经检验,x2=﹣1不是原方程的根,是增根.根据上述思想方法,解下列方程:
=x两边平方,得2x+3=x2,解得x1=3,x2=﹣1.经检验,x2=﹣1不是原方程的根,是增根.根据上述思想方法,解下列方程:
(1)![]() ;
;
(2)![]() =2x.
=2x.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离为 ,旋转角的度数为 .
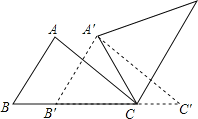
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校对学生进行体育测试,规定参加测试的每名学生从“1.立定跳远、2.1分钟跳绳3.掷实心球、4.50米跑”四个项目中随机抽取两项作为测试项目.
(1)小明同学恰好抽到“立定跳远”、“1分钟跳绳”两项的概率是多少?
(2)据统计,初三一班共12名男生参加了“立定跳远”的测试,他们的成绩如下:
95 100 90 82 90 65 89 74 75 93 92 85
①这组数据的众数是 ,中位数是 ;
②若将不低于90分(含90分)的成绩评为优秀,请你估计初三年级选“立定跳远”的240名男生中成绩为优秀的学生约为多少人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com