
科目:初中数学 来源: 题型:
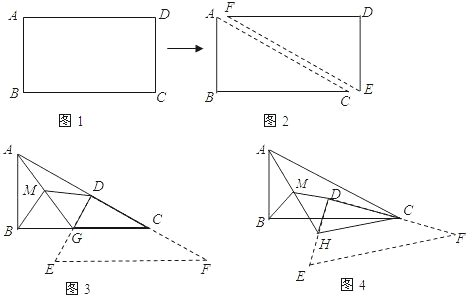
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:044
在同样大小的5张纸片上,画有3个等边三角形和两个正方形,搅匀后任取两张,两个三角形拼成一个菱形,一个三角形与一个正方形拼成一个房子,两个正方形拼成一个矩形,规定菱形为甲胜,房子为乙胜,矩形为和,你认为这个游戏公平吗?
查看答案和解析>>
科目:初中数学 来源:《第4章 统计与概率》2011年单元测试卷(一)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com