
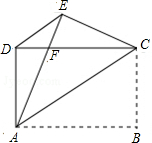
 如图,矩形ABCD中,AB=4,AD=3,把矩形沿直线AC折叠,使点B落在点E处,AE交CD于点F,连接DE.
如图,矩形ABCD中,AB=4,AD=3,把矩形沿直线AC折叠,使点B落在点E处,AE交CD于点F,连接DE.分析 (1)根据矩形的性质、轴对称的性质可得到AD=EC,AE=DC,即可证到△DEC≌△EDA(SSS);
(2)易证AF=CF,设DF=x,则有AF=4-x,然后在Rt△ADF中运用勾股定理就可求出DF的长.
解答 (1)证明:∵四边形ABCD是矩形,
∴AD=BC,AB=DC.
由折叠可得:EC=BC,AE=AB,
∴AD=EC,AE=DC,
在△ADE与△CED中,
$\left\{\begin{array}{l}{AD=CE}\\{DE=ED}\\{DC=EA}\end{array}\right.$,
∴△DEC≌△EDA(SSS).
(2)解:∵∠ACD=∠BAC,∠BAC=∠CAE,
∴∠ACD=∠CAE,
∴AF=CF,
设DF=x,则AF=CF=4-x,
在RT△ADF中,AD2+DF2=AF2,
即32+x2=(4-x)2,
解得;x=$\frac{7}{8}$,
即DF=$\frac{7}{8}$.
点评 本题主要考查了矩形的性质、全等三角形的判定与性质、等腰三角形的判定、轴对称的性质等知识,解决本题的关键是明确折叠的性质,得到相等的线段,角.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:选择题
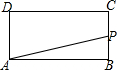 如图,在矩形ABCD中,AB=2,BC=1,动点P从点B出发,沿路线B→C→D作匀速运动,那么△ABP的面积y与点P运动的路程x之间的函数图象大致是( )
如图,在矩形ABCD中,AB=2,BC=1,动点P从点B出发,沿路线B→C→D作匀速运动,那么△ABP的面积y与点P运动的路程x之间的函数图象大致是( )| A. |  | B. | 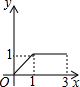 | C. | 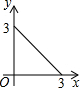 | D. | 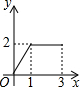 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,若△ABC内任意一点P(x0,y0)经平移后对应点为P1(x0-2,y0-3),现将△ABC作同样的平移得到△A1B1C1
如图,若△ABC内任意一点P(x0,y0)经平移后对应点为P1(x0-2,y0-3),现将△ABC作同样的平移得到△A1B1C1查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,雷达探测器测得六个目标A、B、C、D、E、F出现,按照规定的目标表示方法,目标A、E的位置表示为A(5,30°),E(3,300°),则目标C的位置表示为(6,120°).
如图,雷达探测器测得六个目标A、B、C、D、E、F出现,按照规定的目标表示方法,目标A、E的位置表示为A(5,30°),E(3,300°),则目标C的位置表示为(6,120°).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 利用图形中面积的等量关系可以得到某些数学公式,例如,根据图甲,我们可以得到两数和的平方公式:(a+b)2=a2+2ab+b2.你根据图乙能得到的数学公式是( )
利用图形中面积的等量关系可以得到某些数学公式,例如,根据图甲,我们可以得到两数和的平方公式:(a+b)2=a2+2ab+b2.你根据图乙能得到的数学公式是( )| A. | a2-b2=(a-b)2 | B. | (a+b)2=a2+2ab+b2 | C. | (a-b)2=a2-2ab+b2 | D. | a2-b2=(a+b)(a-b) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com