
【题目】如图,在△ABC中,∠BAC.∠BCA的平分线交于点I,若∠ACB=75°,AI=BC-AC,则∠B的度数为( )
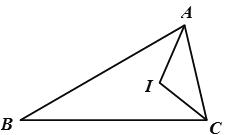
A.30°B.35°C.40°D.45°
【答案】B
【解析】
在BC上取一点D,使得DC=AC,连接BI,DI,结合已知条件得出DB=AI,根据全等三角形的判定可证的△ACI≌△DCI,从而得到BD=ID,设∠IBD=x,利用题目条件表示出∠ABC、∠BAC,最后根据三角形的内角和等于180°即可得出结果.
解:如图所示,在BC上取一点D,使得DC=AC,连接BI,DI

∵AI=BC-AC
∴AI=BD
∵IC是∠ACB的角平分线,AI是∠BAC的角平分线
∴IB是∠ABC的角平分线
∴∠ACI=∠ICB,∠BAI=∠IAC,∠ABI=∠IBC
在△ACI和△ICD中
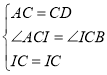
∴△ACI≌△DCI(SAS)
∴AI=ID=BD,∠IAC=∠IDC
∴△IDB是等腰三角形
∴∠IBD=∠BID
∵∠IDC=∠IBD+∠BID=2∠IBD
设∠IBD=x,则∠ABC=2x,∠IAC=2x
则:2x+4x+75°=180°
解得:x=17.5°
∴∠ABC=2×17.5°=35°
故选:B.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列5个结论:①abc<0;②b<a﹣c;③4a+2b+c>0;④2c<3b;⑤a+b<m(am+b),(m≠1的实数)⑥2a+b+c>0,其中正确的结论的有( )
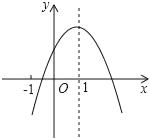
A. 3个 B. 4个 C. 5个 D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O与△ABC的三边AB、BC、AC分别相切于点D、E、F,如果BC边的长为10cm,AD的长为4cm,那么△ABC的周长为_____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D,E分别在AB,AC上,DE∥BC,F是AD上一点,FE的延长线交BC的延长线于点G.求证:
(1)∠EGH>∠ADE;
(2)∠EGH=∠ADE+∠A+∠AEF.
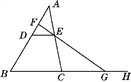
查看答案和解析>>
科目:初中数学 来源: 题型:
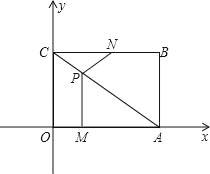
【题目】如图,平面直角坐标系中,四边形OABC为矩形,点A,B的坐标分别为(4,0),(4,3),动点M,N分别从O,B同时出发.以每秒1个单位的速度运动.其中,点M沿OA向终点A运动,点N沿BC向终点C运动.过点M作MP⊥OA,交AC于P,连接NP,已知动点运动了x秒.
(1)求P点的坐标(用含x的代数式表示);
(2)试求△NPC面积S的表达式,并求出面积S的最大值及相应的x值;
(3)设四边形OMPC的面积为S1,四边形ABNP的面积为S2,请你就x的取值范围讨论S1与S2的大小关系并说明理由;
(4)当x为何值时,△NPC是一个等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
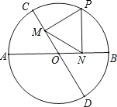
【题目】如图,AB、CD是⊙O的直径,P为![]() 上一个动点(不与B、C重合),PM、PN分别垂直CD、AB,垂足分别为点M、N.若∠AOC=60°,OA=4,则MN的长为________.
上一个动点(不与B、C重合),PM、PN分别垂直CD、AB,垂足分别为点M、N.若∠AOC=60°,OA=4,则MN的长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,∠A=140°,∠D=80°.

(1)如图1,若∠B=∠C,试求出∠C的度数;
(2)如图2,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用![]() ,
,![]() 表示直角三角形的两直角边(
表示直角三角形的两直角边(![]() ),下列四个说法:
),下列四个说法:

①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() .
.
其中说法正确的是 …………………………………………………………( )
A. ①② B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com