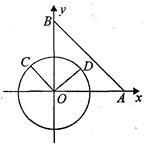
试题分析:(1)设4分钟后小明到达点C,过点C作CD⊥OB于点D,根据旋转的时间可以求得旋转角∠COD,利用三角函数即可求得OD的长,从而求解;
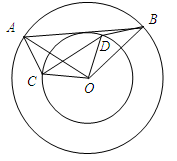
(2)(2)根据所给的高度,能求出OD的长,根据直角三角形中,若直角边是斜边的一半,那么这个直角边所对的角是30°,从而求出转过的∠COD的情况并求解.
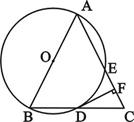
(3)当旋转到E处时,作弦EF⊥AO交AO的延长线于点H,连接OE,OF,此时EF离地面高度为HA,在直角△OEH中,利用三角函数求得∠HOE的度数,则∠EOF的度数即可求得,则旋转的时间即可求得.
(1)设4分钟后小明到达点C,过点C作CD⊥OB于点D,DA即为小明离地的高度,
∵∠COD=

=60°,
∴OD=
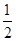
OC=
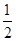
×20=10,
∴DA=20-10+1=11(m).
答:计时4分钟后小明离地面的高度是11m;

(2)∵11<OA=21则小明在摩天轮的下半圆,
∵DA=OA-OD,
∴在Rt△ODC中,OD=21-11=10,OC=20,
∴∠COD=60°,
∴所需时间是

分钟,或

分钟小明离地面的高度将首次达到11m.
(3)∵当旋转到E处时,作弦EF⊥AO交AO的延长线于点H,连接OE,OF,此时EF离地面高度为HA.
当HA=31时,OH=31-1-20=10,
∴OH=
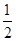
OE,
∴∠HOE=60°,
∴∠FOE=120°.
∵每分钟旋转的角度为:

,
∴由点E旋转到F所用的时间为:

(分钟).
答:在旋转一周的过程中,小明将有8分钟的时间连续保持在离地面31m以上的空中.


 =60°,
=60°,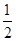 OC=
OC=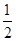 ×20=10,
×20=10,
 分钟,或
分钟,或 分钟小明离地面的高度将首次达到11m.
分钟小明离地面的高度将首次达到11m.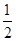 OE,
OE, ,
, (分钟).
(分钟).