
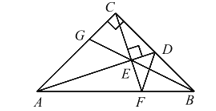
【题目】如图:Rt△ABC 中,AC=BC,∠ACB=90°,D 为 BC 边中点,CF⊥AD 交 AD 于 E,交 AB 于 F,BE交 AC 于 G,连 DF,下列结论:①AC=AF,②CD+DF=AD,③∠ADC=∠BDF,④CE=BE,⑤∠ BED=45°,其中正确的有( )
A. 5 个B. 4 个C. 3 个D. 2 个
【答案】D
【解析】
如图,作BH⊥BC交CF的延长线于H,作BN⊥AD交AD的延长线于N,BM⊥CH于M.想办法证明△ACD≌△CBH(ASA),△BFD≌△BFH(SAS),△ACE≌△CBE(AAS),△CDE≌△BDN(AAS),利用全等三角形的性质一一判断即可.
如图,作BH⊥BC交CF的延长线于H,作BN⊥AD交AD的延长线于N,BM⊥CH于M.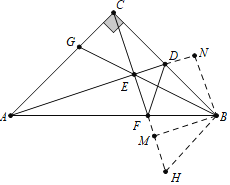
∵AD⊥CF,BH⊥BC,
∴∠ACD=∠CBH=∠AEC=90°,
∵∠CAD+∠ACE=90°,∠ACE+∠BCH=90°,
∴∠CAD=∠BCH,
∵CA=CB,
∴△ACD≌△CBH(ASA),
∴∠ADC=∠H,CD=BH,AD=CH,
∵CD=BD,
∴∠BD=BH,
∵∠FBD=∠FBH=45°,BF=BF,
∴△BFD≌△BFH(SAS),
∴∠H=∠BDF,DF=FH,
∴∠ADC=∠BDF,故③正确,
∵AD=CH,CH=FH+CF=DF+CF,
∵CF>CD,
∴AD≠DF+CD,故②错误,
假设①成立,则∵AE⊥CF,
∴CE=EF,∵CD=DB,
∴DE∥BF,显然与已知矛盾,故①错误,
∵∠CAE=∠BCM,∠AEC=∠CMB,AC=BC,
∴△ACE≌△CBE(AAS),
∴CE=BM,
∵BE>BM,
∴CE≠BE,故④错误,
∵∠CED=∠N=90°,∠CDE=∠BDN,CD=BD,
∴△CDE≌△BDN(AAS),
∴CE=BN,
∵EC=BM,
∴BM=BN,∵BM⊥EH,BN⊥EN,
∴BE平分∠NEH,
∵∠NEH=90°
∴∠BEF=![]() ×90°=45°.故⑤正确.
×90°=45°.故⑤正确.
故选:D.


科目:初中数学 来源: 题型:
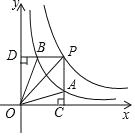
【题目】函数y=![]() 和y=
和y=![]() 在第一象限内的图象如图,点P是y=
在第一象限内的图象如图,点P是y=![]() 的图象上一动点,PC⊥x轴于点C,交y=
的图象上一动点,PC⊥x轴于点C,交y=![]() 的图象于点A,PD⊥y轴于点D,交y=
的图象于点A,PD⊥y轴于点D,交y=![]() 的图象于点B.下面结论:
的图象于点B.下面结论:
①PA与PB始终相等;②△OBP与△OAP的面积始终相等;
③四边形PAOB的面积不变;④PABD=PBAC.
其中一定正确的是_____(把你认为正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
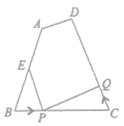
【题目】如图,在四边形![]() 中,
中,![]() 厘米,
厘米,![]() 厘米,
厘米,![]() ,点
,点![]() 为
为![]() 的中点,如果点
的中点,如果点![]() 在线段
在线段![]() 上以3厘米/秒的速度由
上以3厘米/秒的速度由![]() 点向
点向![]() 点运动,同时,点
点运动,同时,点![]() 在线段
在线段![]() 上由
上由![]() 点向
点向![]() 点匀速运动,当点
点匀速运动,当点![]() 的运动速度为__________厘米/秒时,
的运动速度为__________厘米/秒时,![]() 与
与![]() 全等.
全等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解决问题:
小川同学乘坐新开通的C2701次城际列车,它从“北京西”站始发直达终点“大兴机场”站,但因列车行驶的全程分别属于两段不同的路网A段和新开通运营的B段,在两段运行的平均速度有所不同,小川搜集了相关信息填入下表.
线路划分 | A段 | B段(新开通) |
所属全国铁路网 | 京九段 | 京雄城际铁路北京段 |
站间 | 北京西—李营 | 李营—大兴机场 |
里程近似值(单位:km) | 15 | 33 |
运行的平均速度(单位:km/h) | ||
所用时间(单位:h) |
已知C2701次列车在B段运行的平均速度比在A段运行的平均速度快35km/h,在B段运行所用时间是在A段运行所用时间的1.5倍,C2701次列车从“北京西”站到“大兴机场”站全程需要多少小时?(提示:可借助表格解决问题)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2014年巴西世界杯足球赛前夕,某体育用品店购进一批单价为40元的球服,如果按单价60元销售,那么一个月内可售出240套.根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高5元,销售量相应减少20套.设销售单价为x(x≥60)元,销售量为y套.
(1)求出y与x的函数关系式.
(2)当销售单价为多少元时,月销售额为14000元?
(3)当销售单价为多少元时,才能在一个月内获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
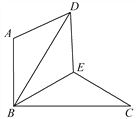
【题目】如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
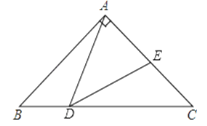
【题目】如图所示,Rt△ABC中,已知∠BAC=90°,AB=AC=2,点D在BC上运动(不能到达点B,C),过点D作∠ADE=45°,DE交AC于点E.
(1)求证:△ABD∽△DCE;
(2)当△ADE是等腰三角形时,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
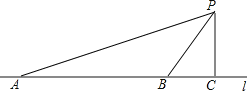
【题目】汽车超速行驶是交通安全的重大隐患,为了有效降低交通事故的发生,许多道路在事故易发路段设置了区间测速如图,学校附近有一条笔直的公路l,其间设有区间测速,所有车辆限速40千米/小时数学实践活动小组设计了如下活动:在l上确定A,B两点,并在AB路段进行区间测速.在l外取一点P,作PC⊥l,垂足为点C.测得PC=30米,∠APC=71°,∠BPC=35°.上午9时测得一汽车从点A到点B用时6秒,请你用所学的数学知识说明该车是否超速.(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin71°≈0.95,cos71°≈0.33,tan71°≈2.90)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com