
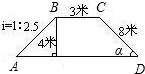
 如图,拦水坝的横断面为梯形ABCD,根据图示数据求:
如图,拦水坝的横断面为梯形ABCD,根据图示数据求: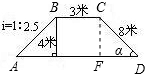 解:(1)过点C作CF⊥AD于F,则CF为梯形的高,
解:(1)过点C作CF⊥AD于F,则CF为梯形的高,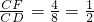 ,
, =
= ,
, =0.4,而tan∠A=
=0.4,而tan∠A=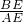 ,
,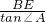 =
=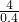 =10;
=10; =13+4
=13+4 ,
,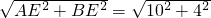 =
=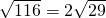 ,
, )米,斜坡AB=2
)米,斜坡AB=2 米.
米.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
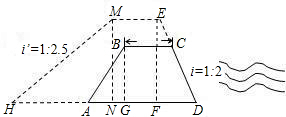 如图,拦水坝的横断面为梯形ABCD,坝顶宽BC=6米,坝高3.2米,为了提高水坝的拦水能力,需将水坝加高2米,并且保持坝顶宽度不变,迎水坡CD的坡度不变,但是背水坡的坡度由原来的i=1:2变成i′=1:2.5(有关数据在图上已注明),求加高后的坝底HD的长为多少?
如图,拦水坝的横断面为梯形ABCD,坝顶宽BC=6米,坝高3.2米,为了提高水坝的拦水能力,需将水坝加高2米,并且保持坝顶宽度不变,迎水坡CD的坡度不变,但是背水坡的坡度由原来的i=1:2变成i′=1:2.5(有关数据在图上已注明),求加高后的坝底HD的长为多少?查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
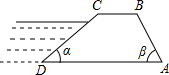 坡度为1:1,坝高为4米,求:
坡度为1:1,坝高为4米,求:查看答案和解析>>
科目:初中数学 来源: 题型:
 坡AB的坡度i=1:3(指坡面的铅直高度AE与水平宽度BE的比),斜坡DC的坡度i=1:1.5,已知该拦水坝的高为6米.
坡AB的坡度i=1:3(指坡面的铅直高度AE与水平宽度BE的比),斜坡DC的坡度i=1:1.5,已知该拦水坝的高为6米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com