
【题目】在如图的正方形网格中,每一个小正方形的边长为1.格点三角形 ABC (顶点是网格线交点的三角形)的顶点 A ,C 的坐标分别是(-4 ,6) ,(-1,4) .
(1)请在图中的网格平面内建立平面直角坐标系;
(2)请画出△ABC 关于 x 轴对称的△A1B1C1 ;并直接写出A1B1C1的坐标.
(3)请在 y 轴上求作一点 P ,使△PB1C 的周长最小,

【答案】(1)作图见解析;(2)作图见解析; A1(-4,-6)、B1(-2,-2)、C1 (-1,-4) ;
(3)作图见解析;P(0,2).
【解析】
(1)根据A点坐标建立平面直角坐标系即可;
(2)分别作出各点关于x轴的对称点,再顺次连接即可;
(3)作出点B关于y轴的对称点B2,连接A、B2交y轴于点P,则P点即为所求.
解:(1)如图所示;
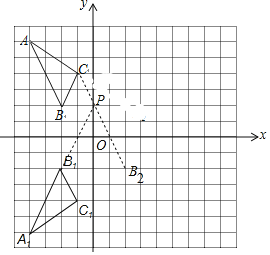
(2)如图所示:A1、B1、C1的坐标是A1(-4,-6)、B1(-2,-2)、C1 (-1,-4)
(3)作点B1关于y轴的对称点B2(2,-2),连接C、B2交y轴于点P,则点P即为所求.
设直线CB2的解析式为y=kx+b(k≠0),
∵C(-1,4),B2(2,-2),![]() ,
,
解得![]()
∴直线CB2的解析式为:y=-2x+2,
∴当x=0时,y=2,
∴P(0,2).


科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,P是BC边上不同于B、C的一动点,过P作PQ⊥AB,垂足为Q,连接AP.

(1)试说明不论点P在BC边上何处时,都有△PBQ与△ABC相似;
(2)若Rt△AQP≌Rt△ACP≌Rt△BQP,求tanB的值;
(3)已知AC=3,BC=4,当BP为何值时,△AQP面积最大,并求出最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点都在方格线的交点(格点)上.
(1)将△ABC绕C点按逆时针方向旋转90°得到△A′B′C′,请在图中画出△A′B′C′.
(2)将△ABC向上平移1个单位,再向右平移5个单位得到△A″B″C″,请在图中画出△A″B″C″.
(3)若将△ABC绕原点O旋转180°,A的对应点A1的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店出售![]() 、
、![]() 两种文具.
两种文具.![]() 文具每套
文具每套![]() 元,
元,![]() 文具每套
文具每套![]() 元,该店开展促销活动,向客户提供两种优惠方案:
元,该店开展促销活动,向客户提供两种优惠方案:
①买一套![]() 文具送一套
文具送一套![]() 文具.
文具.
②![]() 文具和
文具和![]() 文具都按定价的
文具都按定价的![]() 付款.
付款.
现某客户要到该店购买![]() 文具
文具![]() 套,
套,![]() 文具
文具![]() 套(
套(![]() )
)
(![]() )若该客户按方案①购买需付款____________________元(用含
)若该客户按方案①购买需付款____________________元(用含![]() 的代数式表示);若该客户按方案②购买需付款____________________元(用含
的代数式表示);若该客户按方案②购买需付款____________________元(用含![]() 的代数式表示)
的代数式表示)
(![]() )当
)当![]() 时,通过计算说明按哪种方案购买较为合算.
时,通过计算说明按哪种方案购买较为合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形 ABCD 中,∠BAD=α,∠BCD=180°-α,BD 平分∠ABC.
(1)如图,若α=90°,根据教材中一个重要性质直接可得 DA=CD,这个性质是 ;

(2)问题解决:如图,求证:AD=CD;

(3)问题拓展:如图,在等腰△ABC 中,∠BAC=100°,BD 平分∠ABC,求证:BD+AD=BC.

查看答案和解析>>
科目:初中数学 来源: 题型:
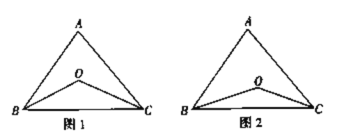
【题目】已知任意一个三角形的三个内角的和是180°,如图1,在ABC中,∠ABC的角平分线BO与∠ACB的角平分线CO的交点为O.
(1)若∠A=70°,求∠BOC的度数;
(2)若∠A=α,求∠BOC的度数;
(3)如图2,若BO、CO分别是∠ABC、∠ACB的三等分线,也就是∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,∠A=α,求∠BOC的度数.
∠ACB,∠A=α,求∠BOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:□ABCD的两边AB,AD的长是关于x的方程x2-mx+![]() -
-![]() =0的两个实数根.
=0的两个实数根.
(1)当m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么□ABCD的周长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示.

(1)根据图象信息,当t= 分钟时甲乙两人相遇,甲的速度为 米/分钟,乙的速度为 米/分钟;
(2)图中点A的坐标为 ;
(3)求线段AB所直线的函数表达式;
(4)在整个过程中,何时两人相距400米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com