
【题目】已知:如图,抛物线y=ax2+bx﹣3与x轴交于A、B两点,与y轴交于点C,O是坐标原点,已知点B的坐标是(3,0),tan∠OAC=3;
(1)求该抛物线的函数表达式;
(2)点P在x轴上方的抛物线上,且∠PAB=∠CAB,求点P的坐标;
(3)若平行于x轴的直线与抛物线交于点M、N(M点在N点左侧),
①若以MN为直径的圆与x轴相切,求该圆的半径;
②若Q(m,4)是直线MN上一动点,当以点C、B、Q为顶点的三角形的面积等于6时,请直接写出符合条件的m值,为 .
【答案】
(1)
解:∵抛物线y=ax2+bx﹣3与y轴交于点C,
∴点C的坐标为(0,﹣3),
∴OC=3,
∵tan∠OAC=3,
∴OA=1,即点A的坐标为(﹣1,0),
将点A和点B的坐标代入得: ![]() ,解得
,解得 ![]() ,
,
∴抛物线的函数表达式是y=x2﹣2x﹣3
(2)
解:∵∠PAB=∠CAB,
∴tan∠PAB=tan∠CAB=3,
∵点P在x轴上方,设点P的横坐标为x,则点P的纵坐标为3(x+1),
∴3(x+1)=x2﹣2x﹣3,得x=﹣1(舍去)或x=6,当x=6时,y=21,
∴点P的坐标为(6,21)
(3)3或11
【解析】解:(3)∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴抛物线的对称轴为直线x=1.
①当直线MN在x轴上方时,设圆的半径为R(R>0),则N(R+1,R),
∴R=( R+1﹣1)2﹣4,解得:R= ![]() (负值舍去),
(负值舍去),
∴R= ![]() .
.
当直线MN在x轴下方时,设圆的半径为r(r>0),
∴N(r+1,﹣r),
∴﹣r=(r+1﹣1)2﹣4,解得:r= ![]() (负值舍去),
(负值舍去),
∴r= ![]() ,
,
∴圆的半径为: ![]() 或
或 ![]() .
.
②设直线BC的解析式为y=kx+b,将点C和点B的坐标代入得: ![]() ,
,
解得k=1,b=﹣3,
∴直线BC的解析式为y=x﹣3.
勾股定理可知:BC= ![]() =3
=3 ![]() .
.
∵△QCB的面积为6,
∴BC边上的高线的长度= ![]() =2
=2 ![]() .
.
如图1所示:即直线BC与y=4的交点为D,当点Q在点D的左侧时,过点Q作QE⊥BC,则EQ=2 ![]()

将y=0代入得直线BC的解析式得:x﹣3=4,解得x=7,
∴点D的坐标为(7,4).
∵QD∥x轴,
∴∠QDC=∠OBC=45°.
∴QD= ![]() QE=
QE= ![]() ×2
×2 ![]() =4.
=4.
∴Q(3,4).
∴m=3.
如图1所示,当Q位于点D的右侧时(Q′处),过点Q′作Q′F⊥BC,垂足为F.则FQ=2 ![]() ,
,
同理可知:DQ′=4.
∴点Q′的坐标为(11,4).
∴m=11.
综上所述,m的值为3或11.
所以答案是:3或11.
【考点精析】认真审题,首先需要了解二次函数的概念(一般地,自变量x和因变量y之间存在如下关系:一般式:y=ax2+bx+c(a≠0,a、b、c为常数),则称y为x的二次函数).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,﹣ ![]() ),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).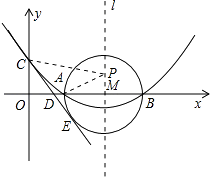
(1)求抛物线的解析式及A、B两点的坐标;
(2)在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP的最小值,若不存在,请说明理由;
(3)以AB为直径的⊙M相切于点E,CE交x轴于点D,求直线CE的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,三角形ABC(记作△ABC)在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是A(﹣2,1),B(﹣3,﹣2),C(1,﹣2),先将△ABC向上平移3个单位长度,再向右平移2个单位长度,得到A1B1C1.
(1)在图中画出△A1B1C1;
(2)点A1,B1,C1的坐标分别为 、 、 ;
(3)若y轴有一点P,使△PBC与△ABC面积相等,求出P点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程:
我们已经学习了一元二次方程的多种解法:如因式分解法,开平方法,配方法和公式法,还可以运用十字相乘法,请从以下一元二次方程中任选两个,并选择你认为适当的方法解这个方程.
①![]() ②
②![]() ③
③![]() ④
④![]()
我选择第 个方程。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某市市民“绿色出行”方式的情况,某校数学兴趣小组以问卷调查的形式,随机调查了某市部分出行市民的主要出行方式(参与问卷调查的市民都只从以下五个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类 | A | B | C | D | E |
出行方式 | 共享单车 | 步行 | 公交车 | 的士 | 私家车 |

根据以上信息,回答下列问题:
(1)参与本次问卷调查的市民共有 人,其中选择B类的人数有 人;
(2)在扇形统计图中,求A类对应扇形圆心角α的度数,并补全条形统计图;
(3)该市约有12万人出行,若将A,B,C这三类出行方式均视为“绿色出行”方式,请估计该市“绿色出行”方式的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知CD⊥DA,DA⊥AB,∠1=∠2.试说明DF∥AE.请你完成下列填空,把证明过程补充完整.
证明:∵ ,
∴∠CDA=90°,∠DAB=90° ( ).
∴∠1+∠3=90°,∠2+∠4=90°.
又∵∠1=∠2,
∴ ( ),
∴DF∥AE ( ).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD. 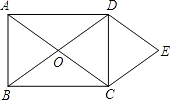
(1)试判断四边形OCED的形状,并说明理由;
(2)若AB=6,BC=8,求四边形OCED的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD的顶点A在原点O处,点B在x轴上,点C的坐标为(6,6),点D在y轴上,动点P,Q各从点A,D同时出发,分别沿AD,DC方向运动,且速度均为每秒1个单位长度. 
(1)探索AQ与BP有什么样的关系?并说明理由;
(2)如图2,当点P运动到线段AD的中点处时,AQ与BP交于点E,求线段CE的长.
(3)如图3,设运动t秒后,点P仍在线段AD上,AQ交BD于F,且△BPQ的面积为S,试求S的最小值,及当S取最小值时∠DPF的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求解答下列各题
(1)已知a、b 互为相反数,c、d 互为倒数,x=(-2)2。
试求x2 -(a + b + c×d) x +(a + b)2015 +(-c×d)2016的值。
(2)已知有理数a、b、c 满足|a-1|+|b-3|+|3c-1|=0,求(a×b×c)178 ÷(a36×b7×c6)的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com