
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷Σ÷±œΏy= ![]() x©¹2”κx÷αΫΜ”ΎΒψAΘ§”κy÷αΫΜ”ΎΒψCΘ§Ψ≠ΙΐAΓΔCΝΫΒψΒΡ≈ΉΈοœΏ”κ÷αΫΜ”ΎΝμ“ΜΒψBΘ®1Θ§0Θ©Θ°
x©¹2”κx÷αΫΜ”ΎΒψAΘ§”κy÷αΫΜ”ΎΒψCΘ§Ψ≠ΙΐAΓΔCΝΫΒψΒΡ≈ΉΈοœΏ”κ÷αΫΜ”ΎΝμ“ΜΒψBΘ®1Θ§0Θ©Θ°
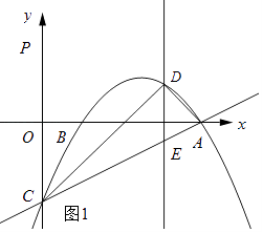
Θ®1Θ©«σΗΟ≈ΉΈοœΏΒΡΫβΈω ΫΘ°
Θ®2Θ©‘Ύ÷±œΏy= ![]() x©¹2…œΖΫΒΡ≈ΉΈοœΏ…œ¥φ‘Ύ“ΜΕ·ΒψDΘ§Ν§Ϋ”ADΓΔCDΘ§…ηΒψDΒΡΚαΉχ±ξΈΣmΘ§ΓςDCAΒΡΟφΜΐΈΣSΘ§«σS”κmΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ«σ≥ωSΒΡΉν¥σ÷ΒΘ°
x©¹2…œΖΫΒΡ≈ΉΈοœΏ…œ¥φ‘Ύ“ΜΕ·ΒψDΘ§Ν§Ϋ”ADΓΔCDΘ§…ηΒψDΒΡΚαΉχ±ξΈΣmΘ§ΓςDCAΒΡΟφΜΐΈΣSΘ§«σS”κmΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ«σ≥ωSΒΡΉν¥σ÷ΒΘ°
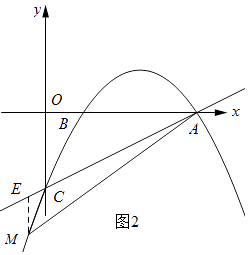
Θ®3Θ©‘Ύ≈ΉΈοœΏ…œ «Ζώ¥φ‘Ύ“ΜΒψMΘ§ ΙΒΟ“‘MΈΣ‘≤–ΡΘ§“‘ ![]() ΈΣΑκΨΕΒΡ‘≤”κ÷±œΏACœύ«–ΘΩ»τ¥φ‘ΎΘ§«κ«σ≥ωΒψMΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΈΣΑκΨΕΒΡ‘≤”κ÷±œΏACœύ«–ΘΩ»τ¥φ‘ΎΘ§«κ«σ≥ωΒψMΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
Θ®4Θ©‘Ύy÷αΒΡ’ΐΑκ÷α…œ¥φ‘Ύ“ΜΒψPΘ§ ΙΓœAPBΒΡ÷ΒΉν¥σΘ§«κ÷±Ϋ”–¥≥ωΒ±ΓœAPBΉν¥σ ±ΒψPΒΡΉχ±ξΘ°
ΓΨ¥πΑΗΓΩ
Θ®1Θ©
ΫβΘΚΑ―x=0¥ζ»κy= ![]() x©¹2ΒΟΘΚy=©¹2Θ°
x©¹2ΒΟΘΚy=©¹2Θ°
ΓύCΘ®0Θ§©¹2Θ©Θ°
Α―y=0¥ζ»κΒΟΘΚ ![]() x©¹2=0Θ§ΫβΒΟΘΚx=4Θ°
x©¹2=0Θ§ΫβΒΟΘΚx=4Θ°
ΓύAΘ®4Θ§0Θ©Θ°
…η≈ΉΈοœΏΒΡΫβΈω ΫΈΣy=aΘ®x©¹4Θ©Θ®x©¹1Θ©Θ§ΫΪΒψCΒΡΉχ±ξ¥ζ»κΒΟΘΚ4a=©¹2Θ§ΫβΒΟΘΚa=©¹ ![]() Θ°
Θ°
Γύ≈ΉΈοœΏΒΡΫβΈω ΫΈΣy=©¹ ![]() x2+
x2+ ![]() x©¹2Θ°
x©¹2Θ°
Θ®2Θ©
ΫβΘΚΙΐΒψDΉςy÷αΒΡΤΫ––œΏΫΜAC”κEΘ§‘ρΒψDΘ®mΘ§©¹ ![]() m2+
m2+ ![]() m©¹2Θ©Θ§EΘ®mΘ§
m©¹2Θ©Θ§EΘ®mΘ§ ![]() m©¹2Θ©Θ°
m©¹2Θ©Θ°
ΓύDE=©¹ ![]() m2+
m2+ ![]() m©¹2©¹Θ®
m©¹2©¹Θ® ![]() m©¹2Θ©=©¹
m©¹2Θ©=©¹ ![]() m2+2mΘ°
m2+2mΘ°
ΓύΓςDACΒΡΟφΜΐS= ![]() ΓΝ4ΓΝΘ®©¹
ΓΝ4ΓΝΘ®©¹ ![]() m2+2mΘ©=©¹m2+4mΘ°
m2+2mΘ©=©¹m2+4mΘ°
ΓύΒ±m=2 ±Θ§SΒΡΉν¥σ÷ΒΈΣ4Θ°
ΓύS”κmΒΡΙΊœΒ ΫΈΣS=©¹m2+4mΘ§ΓςDCAΒΡΉν¥σΟφΜΐΈΣ4Θ°
Θ®3Θ©
ΫβΘΚΓΏΓ―M”κACœύ«–Θ§
ΓύΓςAMCΒΡAC±Ώ…œΒΡΗΏΈΣ ![]() Θ°
Θ°
ΓΏAC=2Θ§OA=4Θ§
ΓύAC=2 ![]() Θ°
Θ°
ΓύSΓςACM= ![]() ΓΝ2
ΓΝ2 ![]() ΓΝ
ΓΝ ![]() =4Θ°
=4Θ°
Β±ΒψM‘ΎACΒΡ…œ ±Θ§”…Θ®2Θ©Ω…÷ΣΘΚΒ±m=2Θ°
ΓύΒψMΒΡΉχ±ξΈΣΘ®2Θ§1Θ©Θ°
Β±ΒψM‘ΎACΒΡœ¬ΖΫ ±Θ§ΙΐΒψMΉςy÷αΒΡΤΫ––œΏΫΜAC”κEΘ§‘ρΒψMΘ®mΘ§©¹ ![]() m2+
m2+ ![]() m©¹2Θ©Θ§EΘ®mΘ§
m©¹2Θ©Θ§EΘ®mΘ§ ![]() m©¹2Θ©Θ°
m©¹2Θ©Θ°
ΓύME=Θ® ![]() m©¹2Θ©©¹Θ®©¹
m©¹2Θ©©¹Θ®©¹ ![]() m2+
m2+ ![]() m©¹2Θ©=
m©¹2Θ©= ![]() m2©¹2mΘ°
m2©¹2mΘ°
ΓύΓςMACΒΡΟφΜΐS= ![]() ΓΝ4ΓΝΘ®
ΓΝ4ΓΝΘ® ![]() m2©¹2mΘ©=m2©¹4mΘ°
m2©¹2mΘ©=m2©¹4mΘ°
Γύm2©¹4m=4Θ§’ϊάμΒΟΘΚm2©¹4m©¹4=0Θ§ΫβΒΟΘΚm=2+2 ![]() Μρm=2©¹2
Μρm=2©¹2 ![]() Θ°
Θ°
ΓύΒψMΒΡΉχ±ξΈΣΘ®2+2 ![]() Θ§
Θ§ ![]() ©¹3Θ©ΜρΘ®2©¹2
©¹3Θ©ΜρΘ®2©¹2 ![]() Θ§©¹
Θ§©¹ ![]() ©¹3Θ©Θ°
©¹3Θ©Θ°
Θ®4Θ©
ΫβΘΚ»γΆΦ3Υυ ΨΘΚΙΐΒψAΉςAEΓΆPBΘ§¥ΙΉψΈΣEΘ°
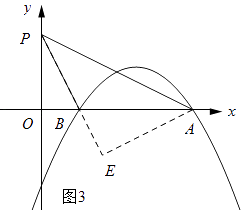
…ηΒψPΒΡΉχ±ξΈΣΘ®0Θ§aΘ©Θ°“άΨίΙ¥Ι…Ε®άμΒΟΘΚAP= ![]() Θ°
Θ°
…η÷±œΏBPΒΡΫβΈω ΫΈΣy=kx+aΘ§ΫΪΒψBΒΡΉχ±ξ¥ζ»κΒΟΘΚk+a=0Θ§ΫβΒΟΘΚk=©¹aΘ°
Γύ÷±œΏPBΒΡΫβΈω ΫΈΣy=©¹ax+aΘ°
…η÷±œΏAEΒΡΫβΈω ΫΈΣy= ![]() x+bΘ§ΫΪΒψAΒΡΉχ±ξ¥ζ»κΒΟΘΚ
x+bΘ§ΫΪΒψAΒΡΉχ±ξ¥ζ»κΒΟΘΚ ![]() +b=0Θ§ΫβΒΟΘΚb=©¹
+b=0Θ§ΫβΒΟΘΚb=©¹ ![]() Θ°
Θ°
Γύ÷±œΏAEΒΡΫβΈω ΫΈΣy= ![]() x©¹
x©¹ ![]() Θ°
Θ°
ΫΪy=©¹ax+a”κy= ![]() x©¹
x©¹ ![]() ΝΣΝΔΘ§ΫβΒΟΘΚx=
ΝΣΝΔΘ§ΫβΒΟΘΚx= ![]() Θ§y=
Θ§y= ![]() Θ°
Θ°
ΓύΒψEΒΡΉχ±ξΈΣΘ® ![]() Θ§
Θ§ ![]() Θ©Θ°
Θ©Θ°
ΓύAE= ![]() Θ°
Θ°
ΓΏsinΓœAPB= ![]() Θ§
Θ§
Γύsin2ΓœAPB= 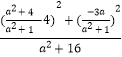 =
= ![]() =
= ![]() =
= ![]() Θ°
Θ°
ΓΏa2+ ![]() Γί2ΓΝa
Γί2ΓΝa ![]() =8Θ§
=8Θ§
ΓύΒ±a= ![]() ±Θ§sinΓœAPB”–Ήν¥σ÷ΒΘ§ΫβΒΟa=2Μρa=©¹2Θ®…α»ΞΘ©Θ°
±Θ§sinΓœAPB”–Ήν¥σ÷ΒΘ§ΫβΒΟa=2Μρa=©¹2Θ®…α»ΞΘ©Θ°
ΓύΒ±a=2 ±Θ§ΓœAPB”–Ήν¥σ÷ΒΘ°
ΓύPΘ®0Θ§2Θ©Θ°
ΓΨΫβΈωΓΩΘ®1Θ©œ»«σΒΟCΘ®0Θ§©¹2Θ©ΓΔAΘ®4Θ§0Θ©Θ§…η≈ΉΈοœΏΒΡΫβΈω ΫΈΣy=aΘ®x©¹4Θ©Θ®x©¹1Θ©Θ§ΫΪΒψCΒΡΉχ±ξ¥ζ»κΩ…«σΒΟaΒΡ÷ΒΘΜΘ®2Θ©ΙΐΒψDΉςy÷αΒΡΤΫ––œΏΫΜAC”κEΘ§‘ρΒψDΘ®mΘ§©¹ ![]() m2+
m2+ ![]() m©¹2Θ©Θ§EΘ®mΘ§
m©¹2Θ©Θ§EΘ®mΘ§ ![]() m©¹2Θ©Θ°‘ρDE=©¹
m©¹2Θ©Θ°‘ρDE=©¹ ![]() m2+2mΘ§»ΜΚσάϊ”Ο»ΐΫ«–ΈΒΡΟφΜΐΙΪ ΫΩ…ΒΟΒΫS”κmΒΡΚ· ΐΙΊœΒ ΫΘ§»ΜΚσάϊ”ΟΕΰ¥ΈΚ· ΐΒΡ–‘÷ Ω…ΒΟΒΫΓςDCAΒΡΟφΜΐΒΡΉν¥σ÷ΒΘΜΘ®3Θ©œ»“άΨίΙ¥Ι…Ε®άμΩ…«σΒΟACΒΡ≥ΛΘ§»ΜΚσΩ…ΒΟΒΫΓςACMΒΡΟφΜΐ=4Θ§Β±ΒψM‘ΎACΒΡ…œ ±Θ§”…Θ®2Θ©Ω…÷ΣMΘ®2Θ§1Θ©Θ°Β±ΒψM‘ΎACΒΡœ¬ΖΫ ±Θ§ΙΐΒψMΉςy÷αΒΡΤΫ––œΏΫΜAC”κEΘ§‘ρΒψMΘ®mΘ§©¹
m2+2mΘ§»ΜΚσάϊ”Ο»ΐΫ«–ΈΒΡΟφΜΐΙΪ ΫΩ…ΒΟΒΫS”κmΒΡΚ· ΐΙΊœΒ ΫΘ§»ΜΚσάϊ”ΟΕΰ¥ΈΚ· ΐΒΡ–‘÷ Ω…ΒΟΒΫΓςDCAΒΡΟφΜΐΒΡΉν¥σ÷ΒΘΜΘ®3Θ©œ»“άΨίΙ¥Ι…Ε®άμΩ…«σΒΟACΒΡ≥ΛΘ§»ΜΚσΩ…ΒΟΒΫΓςACMΒΡΟφΜΐ=4Θ§Β±ΒψM‘ΎACΒΡ…œ ±Θ§”…Θ®2Θ©Ω…÷ΣMΘ®2Θ§1Θ©Θ°Β±ΒψM‘ΎACΒΡœ¬ΖΫ ±Θ§ΙΐΒψMΉςy÷αΒΡΤΫ––œΏΫΜAC”κEΘ§‘ρΒψMΘ®mΘ§©¹ ![]() m2+
m2+ ![]() m©¹2Θ©Θ§EΘ®mΘ§
m©¹2Θ©Θ§EΘ®mΘ§ ![]() m©¹2Θ©Θ°‘ρME=
m©¹2Θ©Θ°‘ρME= ![]() m2©¹2mΘ§»ΜΚσΩ…ΒΟΒΫS”κmΒΡΚ· ΐΙΊœΒ ΫΘ§ΫΪs=4¥ζ»κΩ…«σΒΟmΒΡ÷ΒΘ§¥”ΕχΒΟΒΫΒψMΒΡΉχ±ξΘΜΘ®4Θ©ΙΐΒψAΉςAEΓΆPBΘ§¥ΙΉψΈΣEΘ°…ηΒψPΒΡΉχ±ξΈΣΘ®0Θ§aΘ©Θ°“άΨίΙ¥Ι…Ε®άμΒΟΘΚAP=
m2©¹2mΘ§»ΜΚσΩ…ΒΟΒΫS”κmΒΡΚ· ΐΙΊœΒ ΫΘ§ΫΪs=4¥ζ»κΩ…«σΒΟmΒΡ÷ΒΘ§¥”ΕχΒΟΒΫΒψMΒΡΉχ±ξΘΜΘ®4Θ©ΙΐΒψAΉςAEΓΆPBΘ§¥ΙΉψΈΣEΘ°…ηΒψPΒΡΉχ±ξΈΣΘ®0Θ§aΘ©Θ°“άΨίΙ¥Ι…Ε®άμΒΟΘΚAP= ![]() Θ°»ΜΚσ‘Ό«σΒΟBPΓΔAEΒΡΫβΈω ΫΘ§¥”ΕχΩ…«σΒΟΒψEΒΡΉχ±ξΘ§»ΜΚσ”…sinΓœAPB=
Θ°»ΜΚσ‘Ό«σΒΟBPΓΔAEΒΡΫβΈω ΫΘ§¥”ΕχΩ…«σΒΟΒψEΒΡΉχ±ξΘ§»ΜΚσ”…sinΓœAPB= ![]() Θ§ΒΟΒΫsin2ΓœAPB
Θ§ΒΟΒΫsin2ΓœAPB ![]() Θ§Ι ¥ΥΒ±a=
Θ§Ι ¥ΥΒ±a= ![]() ±Θ§sinΓœAPB”–Ήν¥σ÷ΒΘ§¥”ΕχΩ…«σΒΟaΒΡ÷ΒΘ°
±Θ§sinΓœAPB”–Ήν¥σ÷ΒΘ§¥”ΕχΩ…«σΒΟaΒΡ÷ΒΘ°
ΓΨΩΦΒψΨΪΈωΓΩΙΊ”Ύ±ΨΧβΩΦ≤ιΒΡΕΰ¥ΈΚ· ΐΒΡΆΦœσΚΆΕΰ¥ΈΚ· ΐΒΡ–‘÷ Θ§–η“ΣΝΥΫβΕΰ¥ΈΚ· ΐΆΦœώΙΊΦϋΒψΘΚ1ΓΔΩΣΩΎΖΫœρ2ΓΔΕ‘≥Τ÷α 3ΓΔΕΞΒψ 4ΓΔ”κx÷αΫΜΒψ 5ΓΔ”κy÷αΫΜΒψΘΜ‘ωΦθ–‘ΘΚΒ±a>0 ±Θ§Ε‘≥Τ÷αΉσ±ΏΘ§yΥφx‘ω¥σΕχΦθ–ΓΘΜΕ‘≥Τ÷α”“±ΏΘ§yΥφx‘ω¥σΕχ‘ω¥σΘΜΒ±a<0 ±Θ§Ε‘≥Τ÷αΉσ±ΏΘ§yΥφx‘ω¥σΕχ‘ω¥σΘΜΕ‘≥Τ÷α”“±ΏΘ§yΥφx‘ω¥σΕχΦθ–Γ≤≈ΡήΒΟ≥ω’ΐ»Ζ¥πΑΗΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΥυ Ψ÷–ΒΡΦΗΗωΆΦ–Έ «ΈεΫ«–«ΚΆΥϋΒΡ±δ–ΈΘ°
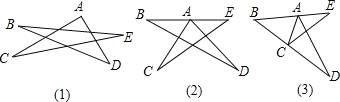
![]() ΆΦΦΉ÷– «“ΜΗωΈεΫ«–«–ΈΉ¥Θ§«σ÷ΛΘΚ
ΆΦΦΉ÷– «“ΜΗωΈεΫ«–«–ΈΉ¥Θ§«σ÷ΛΘΚ![]() ΘΜ
ΘΜ
![]() ΆΦΦΉ÷–ΒΡΒψAœρœ¬“ΤΒΫBE…œ ±
ΆΦΦΉ÷–ΒΡΒψAœρœ¬“ΤΒΫBE…œ ±![]() »γΆΦ““
»γΆΦ““![]() ΈεΗωΫ«ΒΡΚΆ
ΈεΗωΫ«ΒΡΚΆ![]() Φ¥
Φ¥![]() ”–Έό±δΜ·ΘΩ ‘ΥΒΟςάμ”…
”–Έό±δΜ·ΘΩ ‘ΥΒΟςάμ”…
![]() Α―ΆΦ““÷–ΒΡΒψCœρ…œ“ΤΕ·ΒΫBD…œ ±
Α―ΆΦ““÷–ΒΡΒψCœρ…œ“ΤΕ·ΒΫBD…œ ±![]() »γΆΦ±ϊΥυ Ψ
»γΆΦ±ϊΥυ Ψ![]() Θ§ΈεΗωΫ«ΒΡΚΆ
Θ§ΈεΗωΫ«ΒΡΚΆ![]() Φ¥
Φ¥![]() ”–Έό±δΜ·ΘΩ ‘ΥΒΟςάμ”…Θ°
”–Έό±δΜ·ΘΩ ‘ΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
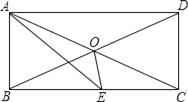
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣAB «Γ―OΒΡœ“Θ§OB=2Θ§ΓœB=30ΓψΘ§C «œ“AB…œΒΡ»Έ“β“ΜΒψ Θ®≤Μ”κΒψAΓΔB÷ΊΚœΘ©Θ§Ν§Ϋ”CO≤Δ―”≥ΛCOΫΜΓ―O”ΎΒψDΘ§Ν§Ϋ”ADΘ° 
Θ®1Θ©œ“≥ΛABΒ»”ΎΘ®ΫαΙϊ±ΘΝτΗυΚ≈Θ©ΘΜ
Θ®2Θ©Β±ΓœD=20Γψ ±Θ§«σΓœBODΒΡΕ» ΐΘΜ
Θ®3Θ©Β±ACΒΡ≥ΛΕ»ΈΣΕύ…Ό ±Θ§“‘AΓΔCΓΔDΈΣΕΞΒψΒΡ»ΐΫ«–Έ”κ“‘BΓΔCΓΔ0ΈΣΕΞΒψΒΡ»ΐΫ«–ΈœύΥΤΘΩ«κ–¥≥ωΫβ¥πΙΐ≥ΧΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΥΡ±Ώ–ΈOABC «ΤΫ––ΥΡ±Ώ–ΈΘ§±ΏOC‘Ύx÷αΒΡΗΚΑκ÷α…œΘ§Ζ¥±»άΐy= ![]() Θ®kΘΦ0Θ©ΒΡΆΦœσΨ≠ΙΐΒψA”κBCΒΡ÷–ΒψFΘ§Ν§Ϋ”AFΓΔOFΘ§»τΓςAOFΒΡΟφΜΐΈΣ9Θ§‘ρkΒΡ÷ΒΈΣ Θ°
Θ®kΘΦ0Θ©ΒΡΆΦœσΨ≠ΙΐΒψA”κBCΒΡ÷–ΒψFΘ§Ν§Ϋ”AFΓΔOFΘ§»τΓςAOFΒΡΟφΜΐΈΣ9Θ§‘ρkΒΡ÷ΒΈΣ Θ° 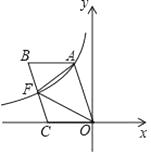
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§–ΓΜΣ‘ΎA¥Πάϊ”ΟΗΏΈΣ1.5ΟΉΒΡ≤βΫ«“«AB≤βΒΟ¬ΞEFΕΞ≤ΩEΒΡ―ωΫ«ΈΣ30ΓψΘ§»ΜΚσ«ΑΫχ30ΟΉΒΫ¥οC¥ΠΘ§”÷≤βΒΟΕΞ≤ΩEΒΡ―ωΫ«ΈΣ60ΓψΘ§«σ¥σ¬ΞEFΒΡΗΏΕ»Θ°Θ®ΫαΙϊΨΪ»ΖΒΫ0.1ΟΉΘ§≤ΈΩΦ ΐΨί ![]() =1.732Θ©
=1.732Θ©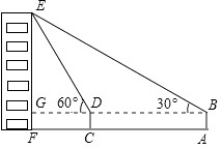
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ±Ώ≥ΛΈΣ1ΒΡΝβ–ΈABCD÷–Θ§ΓœDAB=60ΓψΘ§Ν§Ϋ”Ε‘Ϋ«œΏACΘ§“‘ACΈΣ±ΏΉςΒΎΕΰΗωΝβ–Έ![]() Θ§ Ι
Θ§ Ι![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() Θ§‘Ό“‘
Θ§‘Ό“‘![]() ΈΣ±ΏΉςΒΎ»ΐΗωΝβ–Έ
ΈΣ±ΏΉςΒΎ»ΐΗωΝβ–Έ![]() Θ§ Ι
Θ§ Ι![]() ΘΜΓ≠Θ§Α¥¥ΥΙφ¬…ΥυΉςΒΡΒΎΝυΗωΝβ–ΈΒΡ±Ώ≥ΛΈΣΘ® Θ©
ΘΜΓ≠Θ§Α¥¥ΥΙφ¬…ΥυΉςΒΡΒΎΝυΗωΝβ–ΈΒΡ±Ώ≥ΛΈΣΘ® Θ©

A. 9 B. ![]() C. 27 D.
C. 27 D. ![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§÷±œΏAB”κCDœύΫΜ”ΎOΘ§OEΓΆABΘ§OFΓΆCDΓΘ
(1)ΆΦ÷–”κΓœCOEΜΞ≤ΙΒΡΫ« «___________________ΘΜ (Α―ΖϊΚœΧθΦΰΒΡΫ«ΕΦ–¥≥ωά¥)
(2)»γΙϊΓœAOC =![]() ΓœEOF Θ§«σΓœAOCΒΡΕ» ΐΓΘ
ΓœEOF Θ§«σΓœAOCΒΡΕ» ΐΓΘ

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§ΒψAΓΔBΨυ‘ΎΚ· ΐy= ![]() Θ®kΘΨ0Θ§xΘΨ0Θ©ΒΡΆΦœσ…œΘ§Γ―A”κx÷αœύ«–Θ§Γ―B”κy÷αœύ«–Θ°»τΒψBΒΡΉχ±ξΈΣΘ®1Θ§6Θ©Θ§Γ―AΒΡΑκΨΕ «Γ―BΒΡΑκΨΕΒΡ2±ΕΘ§‘ρΒψAΒΡΉχ±ξΈΣΘ® Θ©
Θ®kΘΨ0Θ§xΘΨ0Θ©ΒΡΆΦœσ…œΘ§Γ―A”κx÷αœύ«–Θ§Γ―B”κy÷αœύ«–Θ°»τΒψBΒΡΉχ±ξΈΣΘ®1Θ§6Θ©Θ§Γ―AΒΡΑκΨΕ «Γ―BΒΡΑκΨΕΒΡ2±ΕΘ§‘ρΒψAΒΡΉχ±ξΈΣΘ® Θ© 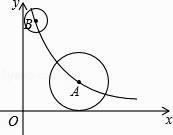
A.Θ®2Θ§2Θ©
B.Θ®2Θ§3Θ©
C.Θ®3Θ§2Θ©
D.Θ®4Θ§ ![]() Θ©
Θ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΨΊ–ΈABCD÷–Θ§ACΓΔBDœύΫΜ”ΎOΘ§AEΤΫΖ÷ΓœBADΫΜBC”ΎEΘ°
Θ®1Θ©«σ÷ΛΘΚΓςABE «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘΜ
Θ®2Θ©»τΓœCAE=15ΓψΘ§«σ÷ΛΘΚΓςABO «Β»±Ώ»ΐΫ«–ΈΘΜ
Θ®3Θ©‘ΎΘ®2Θ©ΒΡΧθΦΰœ¬Θ§«σΓœBOEΒΡΕ» ΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com