
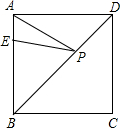
 如图,E是边长为4cm的正方形ABCD的边AB上一点,且AE=1cm,P为对角线BD上的任意一点,则AP+EP的最小值是
如图,E是边长为4cm的正方形ABCD的边AB上一点,且AE=1cm,P为对角线BD上的任意一点,则AP+EP的最小值是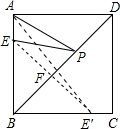 解:作E点关于直线BD的对称点E′,连接AE′,则线段AE′的长即为AP+EP的最小值,
解:作E点关于直线BD的对称点E′,连接AE′,则线段AE′的长即为AP+EP的最小值,| AB2+BE′2 |
| 42+32 |


科目:初中数学 来源: 题型:
 14、如图,O是边长为6的等边三角形ABC内的任意一点,且OD∥BC,交AB于点D,OF∥AB,交AC于F,OE∥AC,交BC于E.则OD+OE+OF的值( )
14、如图,O是边长为6的等边三角形ABC内的任意一点,且OD∥BC,交AB于点D,OF∥AB,交AC于F,OE∥AC,交BC于E.则OD+OE+OF的值( )查看答案和解析>>
科目:初中数学 来源:2012年江苏省苏州市太仓市中考数学模拟试卷(解析版) 题型:选择题
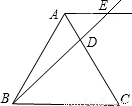
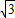
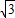
查看答案和解析>>
科目:初中数学 来源:2009年浙江省宁波市奉化市中考数学模拟试卷(解析版) 题型:选择题
 如图,⊙O是边长为1的正方形ABCD的外接圆,P为弧AD上的不同于A、D的任意一点,则PA2+PB2+PC2+PD2的值为( )
如图,⊙O是边长为1的正方形ABCD的外接圆,P为弧AD上的不同于A、D的任意一点,则PA2+PB2+PC2+PD2的值为( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com