
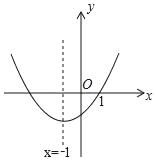
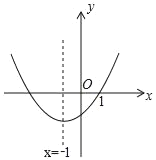
【题目】在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象如图所示,现给以下结论:①abc<0;②c+2a<0;③9a﹣3b+c=0;④a﹣b≥m(am+b)(m为实数);⑤4ac﹣b2<0.其中错误结论的个数有( )
A.1个B.2个C.3个D.4个
【答案】A
【解析】
由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解:①由抛物线可知:a>0,c<0,
对称轴x=﹣![]() <0,
<0,
∴b>0,
∴abc<0,故①正确;
②由对称轴可知:﹣![]() =﹣1,
=﹣1,
∴b=2a,
∵x=1时,y=a+b+c=0,
∴c+3a=0,
∴c+2a=﹣3a+2a=﹣a<0,故②正确;
③(1,0)关于x=﹣1的对称点为(﹣3,0),
∴x=﹣3时,y=9a﹣3b+c=0,故③正确;
④当x=﹣1时,y的最小值为a﹣b+c,
∴x=m时,y=am2+bm+c,
∴am2+bm+c≥a-b+c,
即a﹣b≤m(am+b),故④错误;
⑤抛物线与x轴有两个交点,
∴△>0,
即b2﹣4ac>0,
∴4ac﹣b2<0,故⑤正确;
故选:A.


科目:初中数学 来源: 题型:
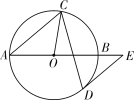
【题目】如图,AB是⊙O的直径,弦CD与AB相交,连接CO,过点D作⊙O的切线,与AB的延长线交于点E,若DE∥AC,∠BAC=40°,则∠OCD的度数为( )
A.65°B.30°C.25°D.20°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与y轴交于点
与y轴交于点![]() .
.
(1)求c的值;
(2)当![]() 时,求抛物线顶点的坐标;
时,求抛物线顶点的坐标;
(3)已知点![]() ,若抛物线
,若抛物线![]() 与线段
与线段![]() 有两个公共点,结合函数图象,求a的取值范围.
有两个公共点,结合函数图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O.
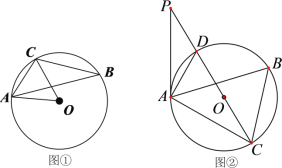
(1)如图①,连接OA,OC,若![]() ,求
,求![]() 的度数;
的度数;
(2)如图②,直径CD的延长线与过点A的切线相交于点P.若![]() ,⊙O的半径为2,求AD,PD的长.
,⊙O的半径为2,求AD,PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD内的一点,连接CP,将线段CP绕点C顺时针旋转90°,得到线段CQ,连接BP,DQ.

(1)、如图a,求证:△BCP≌△DCQ;
(2)、如图,延长BP交直线DQ于点E.
①如图b,求证:BE⊥DQ;
②如图c,若△BCP为等边三角形,判断△DEP的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为推动阳光体育运动的广泛开展,引导学生走向大自然,走到阳光下积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生的鞋号,绘制了如图所示两个统计图,请根据相关信息,解答下列问题:
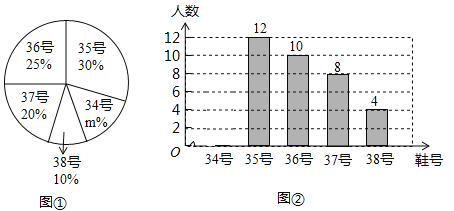
(1)求本次抽样调查的学生人数
(2)通过计算补全条形统计图和扇形统计图;
(3)若学生计划购买200双运动鞋,建议购买35号运动鞋约多少双?
查看答案和解析>>
科目:初中数学 来源: 题型:
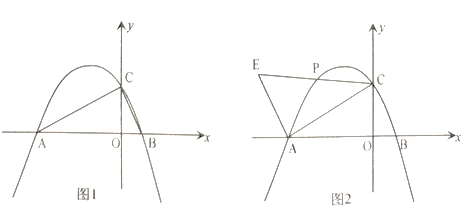
【题目】如图1,已知开口向下的抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() 不小于
不小于![]() .
.
(1)求点![]() 的坐标(用含
的坐标(用含![]() 的代数式表示);
的代数式表示);
(2)求系数![]() 的取值范围;
的取值范围;
请你根据自身能力从![]() 或(4)小题中任选-题作答.
或(4)小题中任选-题作答.
(3)如图2,当![]() 时,
时,![]() 为直线
为直线![]() 上方抛物线上一动点,过点
上方抛物线上一动点,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() 试探究是否存在点
试探究是否存在点![]() ,使得
,使得![]() 的某一个角等于
的某一个角等于![]() 的
的![]() 倍?若存在,求点
倍?若存在,求点![]() 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
(4)如图2,当![]() 时,
时,![]() 为直线
为直线![]() 上方抛物线上一动点,过点
上方抛物线上一动点,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() 抛物线的对称轴与
抛物线的对称轴与![]() 轴交于点
轴交于点![]() 连接
连接![]() 试探究是否存在点
试探究是否存在点![]() 使得
使得![]() 与
与![]() 相似?若存在,求点
相似?若存在,求点![]() 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,正方形![]() 的顶点坐标分别为
的顶点坐标分别为![]() (1,1),
(1,1),![]() (1,-1),
(1,-1),![]() (-1,-1),
(-1,-1),![]() (-1,1),
(-1,1),![]() 轴上有一点
轴上有一点![]() (0,2).作点
(0,2).作点![]() 关于点
关于点![]() 的对称点
的对称点![]() ,作点
,作点![]() 关于点
关于点![]() 的对称点
的对称点![]() ,作点
,作点![]() 关于点
关于点![]() 的对称点
的对称点![]() ,作点
,作点![]() 关于点
关于点![]() 的对称点
的对称点![]() ,作点
,作点![]() 关于点
关于点![]() 的对称点
的对称点![]() ,作点
,作点![]() 关于点
关于点![]() 的对称点
的对称点![]() ,……,按此操作下去,则
,……,按此操作下去,则![]() 的坐标为_____.
的坐标为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com