
【题目】问题探究:
(1)如图①所示是一个半径为![]() ,高为4的圆柱体和它的侧面展开图,AB是圆柱的一条母线,一只蚂蚁从A点出发沿圆柱的侧面爬行一周到达B点,求蚂蚁爬行的最短路程.(探究思路:将圆柱的侧面沿母线AB剪开,它的侧面展开图如图①中的矩形
,高为4的圆柱体和它的侧面展开图,AB是圆柱的一条母线,一只蚂蚁从A点出发沿圆柱的侧面爬行一周到达B点,求蚂蚁爬行的最短路程.(探究思路:将圆柱的侧面沿母线AB剪开,它的侧面展开图如图①中的矩形![]() 则蚂蚁爬行的最短路程即为线段
则蚂蚁爬行的最短路程即为线段![]() 的长)
的长)
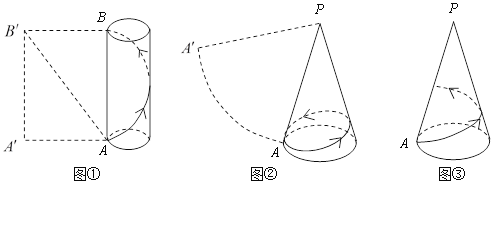
(2)如图②所示是一个底面半径为![]() ,母线长为4的圆锥和它的侧面展开图,PA是它的一条母线,一只蚂蚁从A点出发沿圆锥的侧面爬行一周后回到A点,求蚂蚁爬行的最短路程.
,母线长为4的圆锥和它的侧面展开图,PA是它的一条母线,一只蚂蚁从A点出发沿圆锥的侧面爬行一周后回到A点,求蚂蚁爬行的最短路程.
(3)如图③所示,在②的条件下,一只蚂蚁从A点出发沿圆锥的侧面爬行一周到达母线PA上的一点,求蚂蚁爬行的最短路程.
【答案】(1)蚂蚁爬行的最短路程为5; (2)最短路程为![]() ;(3)蚂蚁爬行的最短距离为
;(3)蚂蚁爬行的最短距离为![]()
【解析】
(1)蚂蚁爬行的最短路程为圆柱侧面展开图即矩形的对角线的长度,由勾股定理可求得;
(2)蚂蚁爬行的最短路程为圆锥展开图中的AA′的连线,可求得△PAA′是等边三角形,则AA′=PA=4;
(3)蚂蚁爬行的最短路程为圆锥展开图中点A到PA的距离.
(1)由题意可知:
![]()
在![]() 中,
中,![]()
即蚂蚁爬行的最短路程为5.
(2)连结![]() 则
则![]() 的长为蚂蚁爬行的最短路程,设
的长为蚂蚁爬行的最短路程,设![]() 为圆锥底面半径,
为圆锥底面半径,![]() 为侧面展开图(扇形)的半径,
为侧面展开图(扇形)的半径,
则![]() 由题意得:
由题意得:![]()
即![]()
![]()
![]() 是等边三角形
是等边三角形
![]() 最短路程为
最短路程为![]()
(3)如图③所示是圆锥的侧面展开图,过![]() 作
作![]() 于点
于点![]() 则线段
则线段![]() 的长就是蚂蚁爬行的最短路程.
的长就是蚂蚁爬行的最短路程.
在Rt△ACP中,
∵∠P=60°,
∴∠PAC=30°
∴PC=![]() PA=
PA=![]() ×4=2
×4=2
∴AC=![]() =
=![]()
![]() 蚂蚁爬行的最短距离为
蚂蚁爬行的最短距离为![]()



科目:初中数学 来源: 题型:
【题目】如图,△ABC和△A'B'C'关于直线MN对称,△A'B'C'和△A″B″C″关于直线EF对称.
(1)画出直线EF;
(2)直线MN与EF相交于点O,试探究∠BOB″与直线MN,EF所夹锐角∠α的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() 为锐角.点
为锐角.点![]() 为射线
为射线![]() 上一动点,连接
上一动点,连接![]() ,以
,以![]() 为一边且在
为一边且在![]() 的右侧作正方形
的右侧作正方形![]() .
.
解答下列问题:
![]() 如果
如果![]() ,
,![]() .
.
①当点![]() 在线段
在线段![]() 上时(与点
上时(与点![]() 不重合),如图2,线段
不重合),如图2,线段![]() 、
、![]() 之间的位置关系为________,数量关系为________.
之间的位置关系为________,数量关系为________.
②当点![]() 在线段
在线段![]() 的延长线上时,如图3,①中的结论是否仍然成立,为什么?
的延长线上时,如图3,①中的结论是否仍然成立,为什么?
![]() 如果
如果![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上运动.试探究:当
上运动.试探究:当![]() 满足一个什么条件时,
满足一个什么条件时,![]() (点
(点![]() 、
、![]() 重合除外)?画出相应图形,并说明理由.(画图不写作法)
重合除外)?画出相应图形,并说明理由.(画图不写作法)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一副三角板的两个直角重叠在一起,∠A=30°,∠C=45°,△COD固定不动,△AOB绕着O点逆时针旋转α°(0°<α<180° ),使两个三角形至少有一组边所在直线垂直,则α=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
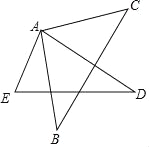
【题目】将一副三角板的两个直角顶点叠放在一起拼成如下的图形.若∠EAB=40°,则∠CAD=____;将△ABC绕直角顶点A旋转时,保持AD在∠BAC的内部,设∠EAC=x°,∠BAD=y°,则x与y的关系是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个长为2,宽为1的矩形ABCD和矩形EFGH如图1所示摆放在直线l上,DE=2,将矩形ABCD绕点D顺时针旋转α角(0°<α<90°),将矩形EFGH绕点E逆时针旋转相同的角度.在旋转的过程中,利用图2思考:当矩形ABCD和矩形EFGH重合部分为正方形时,α=_____°.

查看答案和解析>>
科目:初中数学 来源: 题型:
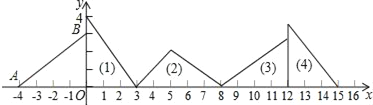
【题目】如图,在平面直角坐标系中,已知点A(﹣4,0)、B(0,3),对△AOB连续作旋转变换依次得到三角形(1)、(2)、(3)、(4)、…,则第(5)个三角形的直角顶点的坐标是_____,第(2018)个三角形的直角顶点的坐标是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一张三角形纸片![]() 如图甲
如图甲![]() ,其中
,其中![]() 将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为
将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为![]() 如图乙
如图乙![]() 再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为
再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为![]() 如图丙
如图丙![]() 原三角形纸片ABC中,
原三角形纸片ABC中,![]() 的大小为______
的大小为______![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】边长相等的下列两种正多边形的组合,不能作平面镶嵌的是( )
A.正方形与正三角形B.正五边形与正三角形
C.正六边形与正三角形D.正八边形与正方形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com