
 如图,E、F分别为平行四边形ABCD两对边AD、BC的中点,AF与BE交于点G,CE与DF交于点H,则图中平行四边形的个数为( )
如图,E、F分别为平行四边形ABCD两对边AD、BC的中点,AF与BE交于点G,CE与DF交于点H,则图中平行四边形的个数为( )| 1 |
| 2 |
| 1 |
| 2 |

|


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案科目:初中数学 来源: 题型:
 | ABC |
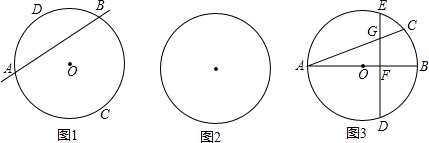 ⊥AB于点F.请找出点C和点E重合的条件,并说明理由.
⊥AB于点F.请找出点C和点E重合的条件,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
 某商场为了吸引顾客,设立一个转盘,如图所示,转盘被平分为16份.规定:当顾客每购买500元金额商品时,就能获得一次转动机会,如果转盘的指针正好对准红、黄、蓝区域,可分别获得100元,50元,20元的购物券,甲顾客购物530元,他获得购物券的概率为
某商场为了吸引顾客,设立一个转盘,如图所示,转盘被平分为16份.规定:当顾客每购买500元金额商品时,就能获得一次转动机会,如果转盘的指针正好对准红、黄、蓝区域,可分别获得100元,50元,20元的购物券,甲顾客购物530元,他获得购物券的概率为| 3 |
| 8 |
| 3 |
| 8 |
| 1 |
| 16 |
| 1 |
| 16 |
查看答案和解析>>
科目:初中数学 来源:第3章《圆》中考题集(24):3.3 圆周角和圆心角的关系(解析版) 题型:解答题
 的中点,弦DE⊥AB于点F.请找出点C和点E重合的条件,并说明理由.
的中点,弦DE⊥AB于点F.请找出点C和点E重合的条件,并说明理由.
查看答案和解析>>
科目:初中数学 来源:第29章《相似形》中考题集(19):29.5 相似三角形的性质(解析版) 题型:解答题
 的中点,弦DE⊥AB于点F.请找出点C和点E重合的条件,并说明理由.
的中点,弦DE⊥AB于点F.请找出点C和点E重合的条件,并说明理由.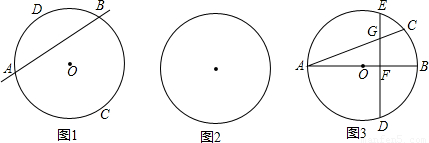
查看答案和解析>>
科目:初中数学 来源:2008年全国中考数学试题汇编《圆》(11)(解析版) 题型:解答题
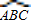 的中点,弦DE⊥AB于点F.请找出点C和点E重合的条件,并说明理由.
的中点,弦DE⊥AB于点F.请找出点C和点E重合的条件,并说明理由.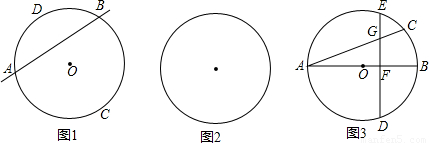
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com