
【题目】如图,一次函数y=kx+b(b=0)的图象与反比例函数y=![]() (m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点A的坐标为(﹣3,4),点B的坐标为(6,n)
(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点A的坐标为(﹣3,4),点B的坐标为(6,n)

(1)求反比例函数和一次函数的解析式;
(2)连接OB,求△AOB的面积;
(3)若kx+b<![]() ,直接写出x的取值范围.
,直接写出x的取值范围.
【答案】(1)![]() ,y=﹣
,y=﹣![]() x+2;(2)9;(3)x>6或﹣3<x<0
x+2;(2)9;(3)x>6或﹣3<x<0
【解析】
(1)根据A的坐标求出反比例函数的解析式,求出B点的坐标,再把A、B的坐标代入y=kx+b,求出一次函数的解析式即可;
(2)先求出点C的坐标,再根据三角形的面积公式求出即可;
(3)根据A、B的坐标和图象得出即可.
解:(1)把A点的坐标(﹣3,4)代入y=![]() 得:m=﹣12,
得:m=﹣12,
即反比例函数的解析式是y=![]() ,
,
把B点的坐标(6,n)代入y=﹣![]() 得:n=﹣2,
得:n=﹣2,
即B点的坐标是(6,﹣2),
把A、B的坐标代入y=kx+b得:![]() ,
,
解得:k=﹣![]() ,b=2,
,b=2,
所以一次函数的解析式是y=﹣![]() x+2;
x+2;

(2)设一次函数y=﹣![]() x+2与x轴的交点是C,
x+2与x轴的交点是C,
y=﹣![]() x+2,当y=0时,x=3,
x+2,当y=0时,x=3,
即OC=3,
∵A(﹣3,4),B(6,﹣2),
∴△AOB的面积S=S△AOC+S△BOC=![]() =9;
=9;
(3)当kx+b<![]() 时x的取值范围是x>6或﹣3<x<0.
时x的取值范围是x>6或﹣3<x<0.


科目:初中数学 来源: 题型:
【题目】定义:对于给定的两个函数,任取自变量x的一个值,当x<0时,它们对应的函数值互为相反数;当x≥0时,它们对应的函数值相等,我们称这样的两个函数互为相关函数.例如:一次函数y=x﹣1,它的相关函数为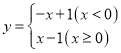 .
.
(1)已知点A(﹣5,8)在一次函数y=ax﹣3的相关函数的图象上,求a的值;
(2)已知二次函数![]() .
.
①当点B(m,![]() )在这个函数的相关函数的图象上时,求m的值;
)在这个函数的相关函数的图象上时,求m的值;
②当﹣3≤x≤3时,求函数![]() 的相关函数的最大值和最小值;
的相关函数的最大值和最小值;
(3)在平面直角坐标系中,点M,N的坐标分别为(﹣![]() ,1),(
,1),(![]() ,1}),连结MN.直接写出线段MN与二次函数
,1}),连结MN.直接写出线段MN与二次函数![]() 的相关函数的图象有两个公共点时n的取值范围.
的相关函数的图象有两个公共点时n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
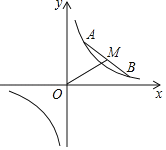
【题目】如图,在平面直角坐标系中,点![]() ,
,![]() 在反比例函数
在反比例函数![]() 的图象上运动,且始终保持线段
的图象上运动,且始终保持线段![]() 的长度不变.
的长度不变.![]() 为线段
为线段![]() 的中点,连接
的中点,连接![]() .则线段
.则线段![]() 长度的最小值是_____(用含
长度的最小值是_____(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
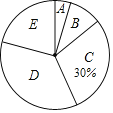
【题目】某校九年级学生参加了中考体育考试.为了了解该校九年级(1)班同学的中考体育成绩情况,对全班学生的中考体育成绩进行了统计,并绘制出以下不完整的频数分布表(如表)和扇形统计图(如图),根据图表中的信息解答下列问题:
分组 | 分数段(分) | 频数 |
A | 36≤x<41 | 2 |
B | 41≤x<46 | 5 |
C | 46≤x<51 | 15 |
D | 51≤x<56 | m |
E | 56≤x<61 | 10 |
(1)m的值为 ;
(2)该班学生中考体育成绩的中位数落在 组;(在A、B、C、D、E中选出正确答案填在横线上)
(3)该班中考体育成绩满分共有3人,其中男生2人,女生1人,现需从这3人中随机选取2人到八年级进行经验交流,请用“列表法”或“画树状图法”求出恰好选到一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
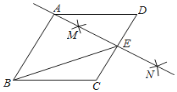
【题目】如图,在菱形![]() 中,
中,![]() ,按以下步骤作图:①分别以点
,按以下步骤作图:①分别以点![]() 和点
和点![]() 为圆心,为圆心,大于号
为圆心,为圆心,大于号![]() 的长为半径面狐,两弧交于点
的长为半径面狐,两弧交于点![]() ,
,![]() :②做直线
:②做直线![]() ,且
,且![]() 恰好经过点
恰好经过点![]() ,与
,与![]() 交于点
交于点![]() ,连接
,连接![]() ,则
,则![]() 的值为( )
的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察等式:1+2+22=23-1;1+2+22+23=24-1;1+2+22+23+24=25-1;若1+2+22+…+29=210-1=m,则用含 m 的式子表示 211+212 + …+218+219 的结果是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
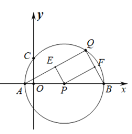
【题目】如图,在平面直角坐标系![]() 中,以
中,以![]() 为圆心作⊙
为圆心作⊙![]() ,⊙
,⊙![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,![]() 为⊙
为⊙![]() 上不同于
上不同于![]() 、
、![]() 的任意一点,连接
的任意一点,连接![]() 、
、![]() ,过
,过![]() 点分别作
点分别作![]() 于
于![]() ,
,![]() 于
于![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() ,
,![]() .当
.当![]() 点在⊙
点在⊙![]() 上顺时针从点
上顺时针从点![]() 运动到点
运动到点![]() 的过程中,下列图象中能表示
的过程中,下列图象中能表示![]() 与
与![]() 的函数关系的部分图象是( )
的函数关系的部分图象是( )
A.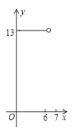 B.
B.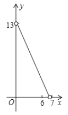 C.
C.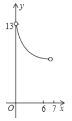 D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图AM∥BN,C是BN上一点, BD平分∠ABN且过AC的中点O,交AM于点D,DE⊥BD,交BN于点E.

(1)求证:△ADO≌△CBO.
(2)求证:四边形ABCD是菱形.
(3)若DE = AB = 2,求菱形ABCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com