
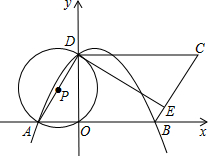
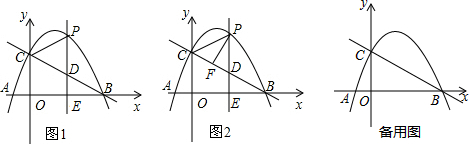
 ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxoyÖŠ£¬OĪŖŌµć£¬?ABCDµÄ±ßABŌŚxÖįÉĻ£¬µćDŌŚyÖįÉĻ£¬µćAµÄ×ų±źĪŖ£Ø-2£¬0£©£¬AB=6£¬”ĻBAD=60”ć£¬µćEŹĒBC±ßÉĻŅ»µć£¬CE=3EB£¬”ŃP¹żA”¢O”¢DČżµć£¬Å×ĪļĻßy=ax2+bx+c¹żµćA”¢B”¢DČżµć£®
ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxoyÖŠ£¬OĪŖŌµć£¬?ABCDµÄ±ßABŌŚxÖįÉĻ£¬µćDŌŚyÖįÉĻ£¬µćAµÄ×ų±źĪŖ£Ø-2£¬0£©£¬AB=6£¬”ĻBAD=60”ć£¬µćEŹĒBC±ßÉĻŅ»µć£¬CE=3EB£¬”ŃP¹żA”¢O”¢DČżµć£¬Å×ĪļĻßy=ax2+bx+c¹żµćA”¢B”¢DČżµć£®·ÖĪö £Ø1£©ĻČČ·¶Ø³öµćBµÄ×ų±ź£¬½ų¶ųĒó³öµćDµÄ×ų±ź£¬×īŗóÓĆ“ż¶ØĻµŹż·ØĒó³öÅ×ĪļĻß½āĪöŹ½£»
£Ø2£©ĻČĒó³öCE=3£¬ĄūÓĆĮ½±ß¶ŌÓ¦³É±ČĄż£¬¼Š½ĒĻąµČÅŠ¶Ļ³ö”÷OAD”×”÷ECD¼“æÉµĆ³ö”ĻODA=”ĻEDC£¬¼“æÉµĆ³ö”ĻODE=90”ć£¬½įĀŪµĆÖ¤£»
£Ø3£©ĻČĄūÓĆŠż×ŖĒó³öµćE'µÄ×ų±ź£¬×īŗóÅŠ¶ØµćE'ŹĒ·ńŌŚÅ×ĪļĻßÉĻ£»
£Ø4£©·ÖČżÖÖĒéæö£¬ĄūÓĆĻ߶ĪµÄÖŠµć×ų±ź¹«Ź½£¬ŗĶĘ½ŠŠĖıߊĪµÄ¶Ō½ĒĻß»„ĻąĘ½·Ö½ØĮ¢·½³ĢĒó½ā¼“æÉµĆ³ö½įĀŪ£®
½ā“š ½ā£ŗ£Ø1£©”ßA£Ø-2£¬0£©£¬AB=6£¬
”ąB£Ø4£¬0£©£¬
”ąOB=4£¬
”ßDO”ĶAB£¬”ĻBAD=60”ć£¬
”ąOD=OAtan60”ć=2$\sqrt{3}$£¬
”ąD£Ø0£¬2$\sqrt{3}$£©£¬
”ßÅ×ĪļĻßy=ax2+bx+c¹żµćA£¬B£¬D£»
”ą$\left\{\begin{array}{l}{4a+2b+c=0}\\{16a+4b+c=0}\\{c=2\sqrt{3}}\end{array}\right.$£¬
”ą$\left\{\begin{array}{l}{a=\frac{\sqrt{3}}{4}}\\{b=-\frac{\sqrt{3}}{2}}\\{c=2\sqrt{3}}\end{array}\right.$£¬
”ąÅ×ĪļĻߵĽāĪöŹ½ĪŖy=$\frac{\sqrt{3}}{4}$x2-$\frac{\sqrt{3}}{2}$x+2$\sqrt{3}$£»
£Ø2£©A£Ø-2£¬0£©£¬
”ąOA=2£¬
ŌŚRt”÷AODÖŠ£¬”ĻBAD=60”ć£¬
”ąOD=2$\sqrt{2}$£¬AD=4£¬
”ßĖıߊĪABCDŹĒĘ½ŠŠĖıߊĪ£¬
”ą”ĻCAD=”ĻC=60”ć£¬CD=AB=6£¬BC=AD=4£¬
”ßCE=3EB£¬
”ąCE=3£¬
”ą$\frac{OA}{AD}=\frac{2}{4}=\frac{1}{2}$£¬$\frac{CE}{CD}=\frac{3}{6}=\frac{1}{2}$£¬
”ą$\frac{OA}{AD}=\frac{CE}{CD}$£¬”ß”ĻOAD=”ĻC£¬
”ą”÷OAD”×”÷ECD£¬
”ą”ĻODA=”ĻEDC£¬
”ß”ĻODC=90”ć£¬
”ą”ĻADE=”ĻODA+”ĻODE=”ĻEDC+”ĻODE=90”ć£¬
”ßµćDŌŚ”ŃPÉĻ£¬
”ąDEŹĒ”ŃPµÄĒŠĻߣ»
£Ø3£©µćE'²»ŌŚÅ×ĪļĻßÉĻ£¬ĄķÓÉ£ŗČēĶ¼1£¬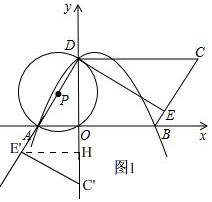 ”ß”ĻADE=90”ć£¬
”ß”ĻADE=90”ć£¬
”ąµćE'ĀäŌŚDAµÄŃÓ³¤ĻßÉĻ£¬µćC'ĀäŌŚyÖįÉĻ£¬
”ąC'£Ø0£¬-6£©£¬
ÓÉŠż×ŖÖŖ£¬”ĻDC'E'=”ĻC=60”ć£¬C'E'=CE=3£¬
¹żµćE'×÷E'H”ĶDC'ÓŚH£¬
”ąE'H=C'E'sin60”ć=$\frac{3\sqrt{3}}{2}$£¬C'H=C'E'cos60”ć=$\frac{3}{2}$£¬
”ąOH=DC'-C'H-OD=$\frac{9}{2}-2\sqrt{3}$£¬
”ßµćE'ĀäŌŚµŚČżĻóĻŽ£¬
”ąE'£Ø-$\frac{3\sqrt{3}}{2}$£¬2$\sqrt{3}$-$\frac{9}{2}$£©£¬
µ±x=-$\frac{3\sqrt{3}}{2}$Ź±£¬y=-$\frac{\sqrt{3}}{4}$”Į£Ø-$\frac{3\sqrt{3}}{2}$£©2+$\frac{\sqrt{3}}{2}$”Į£Ø-$\frac{3\sqrt{3}}{2}$£©+2$\sqrt{3}$=$\frac{5\sqrt{3}}{16}$-$\frac{9}{4}$”Ł2$\sqrt{3}$-$\frac{9}{4}$£¬
”ąµćE'²»ŌŚÅ×ĪļĻßÉĻ£»
£Ø4£©ČēĶ¼2£¬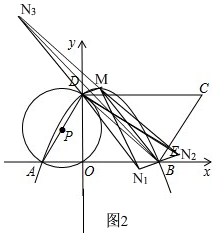 ÓÉ£Ø1£©ÖŖ£¬Å×ĪļĻߵĽāĪöŹ½ĪŖy=$\frac{\sqrt{3}}{4}$x2-$\frac{\sqrt{3}}{2}$x+2$\sqrt{3}$£»
ÓÉ£Ø1£©ÖŖ£¬Å×ĪļĻߵĽāĪöŹ½ĪŖy=$\frac{\sqrt{3}}{4}$x2-$\frac{\sqrt{3}}{2}$x+2$\sqrt{3}$£»
”ąM£Ø1£¬$\frac{7\sqrt{3}}{4}$£©£¬
”ßB£Ø4£¬0£©£¬D£Ø0£¬2$\sqrt{3}$£©£¬
ÉčN£Øm£¬n£©£¬
”ßŅŌµćB”¢D”¢M”¢NĪŖ¶„µćµÄĖıߊĪĪŖĘ½ŠŠĖıߊĪ£¬
¢Łµ±BDÓėMNŹĒ¶Ō½ĒĻߏ±£¬
”ą$\frac{1}{2}$£Øm+1£©=$\frac{1}{2}$”Į4£¬$\frac{1}{2}$£Øn+$\frac{7\sqrt{3}}{4}$£©=$\frac{1}{2}$”Į2$\sqrt{3}$£¬
”ąm=3£¬n=-$\frac{\sqrt{3}}{4}$£¬
”ąN1£Ø3£¬-$\frac{\sqrt{3}}{4}$£©£¬
¢Śµ±BMÓėDNŹĒ¶Ō½ĒĻߏ±£¬Ķ¬¢ŁµÄ·½·ØµĆ£¬N2£Ø5£¬$\frac{\sqrt{3}}{4}$£©£¬
¢Ūµ±BNÓėDMŹĒ¶Ō½ĒĻߏ±£¬Ķ¬¢ŁµÄ·½·ØµĆ£¬N3£Ø-3£¬$\frac{17\sqrt{3}}{4}$£©£®
µćĘĄ “ĖĢāŹĒ¶ž“ĪŗÆŹż×ŪŗĻĢā£¬Ö÷ŅŖæ¼²éĮĖ“ż¶ØĻµŹż·Ø£¬ĻąĖĘČż½ĒŠĪµÄÅŠ¶ĻŗĶŠŌÖŹ£¬Ę½ŠŠĖıߊĪµÄŠŌÖŹ£¬Ö±½ĒČż½ĒŠĪµÄŠŌÖŹ£¬Šż×ŖµÄŠż×Ŗ£¬½ā£Ø1£©µÄ¹Ų¼üŹĒĒó³öµćDµÄ×ų±ź£¬½ā£Ø2£©µÄ¹Ų¼üŹĒÅŠ¶Ļ³ö”÷OAD”×”÷ECD£¬½ā£Ø3£©µÄ¹Ų¼üŹĒĄūÓĆŠż×ŖČ·¶Ø³öµćE'µÄ×ų±ź£¬½ā£Ø4£©µÄ¹Ų¼üŹĒ·ÖĄąĢÖĀŪµÄĖ¼Ļė½ā¾öĪŹĢā£®


 Ķ¬²½Į·Ļ°Ēæ»ÆĶŲÕ¹ĻµĮŠ“š°ø
Ķ¬²½Į·Ļ°Ēæ»ÆĶŲÕ¹ĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
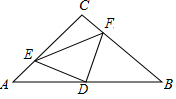 ČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬”ĻC=90”ć£¬AC=BC=4£¬DŹĒABµÄÖŠµć£¬µćE”¢F·Ö±šŌŚAC”¢BC±ßÉĻŌĖ¶Æ£ØµćE²»ÓėµćA”¢CÖŲŗĻ£©£¬ĒŅ±£³ÖAE=CF£¬Į¬½ÓDE”¢DF”¢EF£®
ČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬”ĻC=90”ć£¬AC=BC=4£¬DŹĒABµÄÖŠµć£¬µćE”¢F·Ö±šŌŚAC”¢BC±ßÉĻŌĖ¶Æ£ØµćE²»ÓėµćA”¢CÖŲŗĻ£©£¬ĒŅ±£³ÖAE=CF£¬Į¬½ÓDE”¢DF”¢EF£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{6}$ | B£® | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | C£® | $\sqrt{2}$”Į$\sqrt{5}$=$\sqrt{10}$ | D£® | $\sqrt{8}$”Ā$\sqrt{2}$=4 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
 ČēĶ¼ĖłŹ¾£¬ÕŪµž¾ŲŠĪµÄŅ»±ßAD£¬Ź¹µćDĀäŌŚ±ßBCµÄµćF“¦£¬ŅŃÖŖAB=8cm£¬BC=10cm£¬ŌņECµÄ³¤ĪŖ3cm£®
ČēĶ¼ĖłŹ¾£¬ÕŪµž¾ŲŠĪµÄŅ»±ßAD£¬Ź¹µćDĀäŌŚ±ßBCµÄµćF“¦£¬ŅŃÖŖAB=8cm£¬BC=10cm£¬ŌņECµÄ³¤ĪŖ3cm£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com