
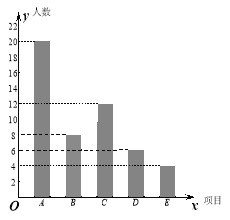
【题目】(本题满分8分)东营市为进一步加强和改进学校体育工作,切实提高学生体质健康水平,决定推进“一校一球队、一级一专项、一人一技能”活动计划.某校决定对学生感兴趣的球类项目(A:足球, B:篮球, C:排球,D:羽毛球,E:乒乓球)进行问卷调查,学生可根据自己的喜好选修一门,李老师对某班全班同学的选课情况进行统计后,制成了两幅不完整的统计图(如图).

(1)求出该班学生人数;
(2)将统计图补充完整;
(3)若该校共有学生3500名,请估计有多少人选修足球?
(4)该班班委5人中,1人选修篮球,3人选修足球,1人选修排球,李老师要从这5人中任选2人了解他们对体育选修课的看法,请你用列表或画树状图的方法,求选出的2人恰好1人选修篮球,1人选修足球的概率.
【答案】(1)50人;
(2)图形见解析;
(3)有1400人选修足球;
(4)选出的2人恰好1人选修篮球,1人选修足球的概率是![]() .
.
【解析】
试题(1)由B:8人,占16%,用8去除以16%得总人数50;
用D的人数6除以50得D所占的百分比,1-16%-24%-12%-8%=40%,即为A的百分比;50分别去乘以A、C、E的百分比即得各组的人数,补图即可;
用总人数3500乘以足球所占的比即可;
列表即可求得概率.
试题解析:(1)该班人数:8÷0.16=50(人);
(2)如图所示;

(3)选修足球的人数:3500×![]() =1400(人);
=1400(人);
(4)用“1”代表篮球,“2、3、4”代表足球,“5”代表排球,可以用下表列举出所有可能出现的结果.
1 | 2 | 3 | 4 | 5 | |
1 | (2,1) | (3,1) | (4,1) | (5,1) | |
2 | (1,2) | (3,2) | (4,2) | (5,2) | |
3 | (1,3) | (2,3) | (4,3) | (5,3) | |
4 | (1,4) | (2,4) | (3,4) | (5,4) | |
5 | (1,5) | (2,5) | (3,5) | (4,5) |
由图可以看出,可能出现的结果有20种,并且它们出现的可能性相等.选出的两人1人选修篮球,1人选修足球(记为事件A)的结果有6种,即(1,2),(1,3),(1,4),(2,1),(3,1),(4,1),所以P(A)=![]()


科目:初中数学 来源: 题型:
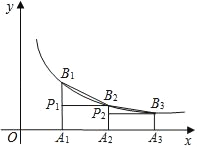
【题目】如图,已知点A1、A2、A3、…、An在x轴上,且OA1=A1A2=A2A3=…=An﹣1An=1,分别过点A1、A2、A3、An作x轴的垂线,交反比例函数y=![]() (x>0)的图象于点B1、B2、B3、…、Bn,过点B2作B2P1⊥A1B1于点P1,过点B3作B3P2⊥A2B2于点P2,…,若记△B1P1B2的面积为S1,△B2P2B3的面积为S2,…,△BnPnBn+1的面积为Sn,则S1+S2+…+S2018=_____.
(x>0)的图象于点B1、B2、B3、…、Bn,过点B2作B2P1⊥A1B1于点P1,过点B3作B3P2⊥A2B2于点P2,…,若记△B1P1B2的面积为S1,△B2P2B3的面积为S2,…,△BnPnBn+1的面积为Sn,则S1+S2+…+S2018=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
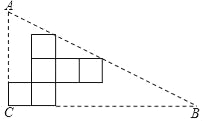
【题目】如图,在Rt△ABC纸片上可按如图所示方式剪出一正方体表面展开图,直角三角形的两直角边与正方体展开图左下角正方形的边共线,斜边恰好经过两个正方形的顶点,已知BC=24cm,则这个展开图可折成的正方体的体积为_____cm3.
查看答案和解析>>
科目:初中数学 来源: 题型:
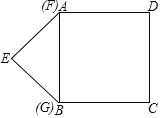
【题目】如图,边长为4个单位长度的正方形ABCD的边AB与等腰直角三角形EFG的斜边FG重合,△EFG以每秒1个单位长度的速度沿BC向右匀速运动(保持FG⊥BC),当点E运动到CD边上时△EFG停止运动,设△EFG的运动时间为t秒,△EFG与正方形ABCD重叠部分的面积为S,则S关于t的函数大致图象为( )
A. 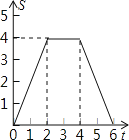 B.
B. 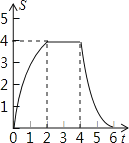 C.
C. 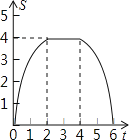 D.
D. 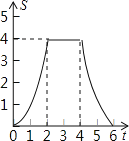
查看答案和解析>>
科目:初中数学 来源: 题型:
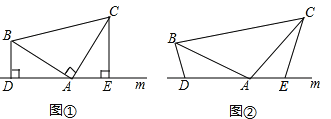
【题目】(1)如图①,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人5场10次投篮命中次数如图:
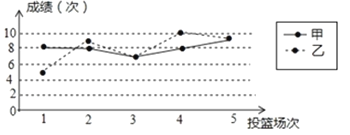
(1)根据图形填表:
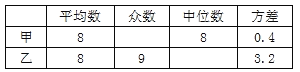
(2)①教练根据这5个成绩,选择甲参加投篮比赛,理由是什么?
②如果乙再投篮1场,命中8次,那么乙的投篮成绩的方差将会怎样变化?(“变大”“变小”或“不变”)
查看答案和解析>>
科目:初中数学 来源: 题型:
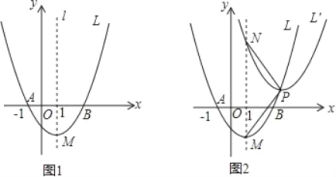
【题目】如图1,已知抛物线L:y=ax2+bx﹣1.5(a>0)与x轴交于点A(-1,0)和点B,顶点为M,对称轴为直线l:x=1.
(1)直接写出点B的坐标及一元二次方程ax2+bx﹣1.5=0的解.
(2)求抛物线L的解析式及顶点M的坐标.
(3)如图2,设点P是抛物线L上的一个动点,将抛物线L平移.使它的頂点移至点P,得到新抛物线L′,L′与直线l相交于点N.设点P的横坐标为m
①当m=5时,PM与PN有怎样的数量关系?请说明理由.
②当m为大于1的任意实数时,①中的关系式还成立吗?为什么?
③是否存在这样的点P,使△PMN为等边三角形?若存在.请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
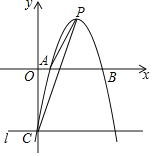
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象与x轴交于A、B两点,与y轴交于点C,其顶点为P,连接PA、AC、CP,过点C作y轴的垂线l.
的图象与x轴交于A、B两点,与y轴交于点C,其顶点为P,连接PA、AC、CP,过点C作y轴的垂线l.
![]() 求点P,C的坐标;
求点P,C的坐标;
![]() 直线l上是否存在点Q,使
直线l上是否存在点Q,使![]() 的面积等于
的面积等于![]() 的面积的2倍?若存在,求出点Q的坐标;若不存在,请说明理由.
的面积的2倍?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com