
【题目】在平面直角坐标系中,已知![]() 、
、![]() ,B为y轴上的动点,以AB为边构造
,B为y轴上的动点,以AB为边构造![]() ,使点C在x轴上,
,使点C在x轴上,![]() 为BC的中点,则PM的最小值为______.
为BC的中点,则PM的最小值为______.
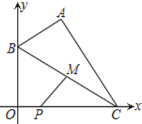
【答案】![]()
【解析】
如图,作AH⊥y轴于H,CE⊥AH于E.则四边形CEHO是矩形,OH=CE=4,由△AHB∽△CEA,得![]() ,推出
,推出![]() ,推出AE=2BH,设BH=x则AE=2x,推出B(0,4﹣x),C(2+2x,0),由BM=CM,推出M(1+x,
,推出AE=2BH,设BH=x则AE=2x,推出B(0,4﹣x),C(2+2x,0),由BM=CM,推出M(1+x,![]() ),可得PM
),可得PM![]() ,由此即可解决问题.
,由此即可解决问题.
如图,作AH⊥y轴于H,CE⊥AH于E.则四边形CEHO是矩形,OH=CE=4.
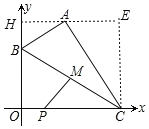
∵∠BAC=∠AHB=∠AEC=90°,∴∠ABH+∠HAB=90°,∠HAB+∠EAC=90°,∴∠ABH=∠EAC,∴△AHB∽△CEA,∴![]() ,∴
,∴![]() ,∴AE=2BH,设BH=x则AE=2x,∴OC=HE=2+2x,OB=4﹣x,∴B(0,4﹣x),C(2+2x,0).
,∴AE=2BH,设BH=x则AE=2x,∴OC=HE=2+2x,OB=4﹣x,∴B(0,4﹣x),C(2+2x,0).
∵BM=CM,∴M(1+x,![]() ).
).
∵P(1,0),∴PM![]() ,∴x
,∴x![]() 时,PM有最小值,最小值为
时,PM有最小值,最小值为![]() .
.
故答案为:![]() .
.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
【题目】如图,点P是菱形ABCD边上的一动点,它从点A出发沿着A→B→C→D路径匀速运动到点D,设△PAD的面积为y,P点的运动时间为x,则y关于x的函数图象大致为( )
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
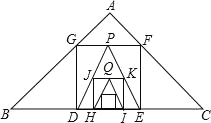
【题目】如图,已知在Rt△ABC中,AB=AC=3![]() ,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形…依次进行下去,则第2014个内接正方形的边长为____.
,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形…依次进行下去,则第2014个内接正方形的边长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
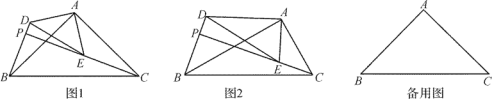
【题目】△ABC和△ADE是有公共顶点的三角形,∠BAC=∠DAE=90°,点P为射线BD,CE的交点.
(1) ①如图1,∠ADE=∠ABC=45°,求证:∠ABD=∠ACE.
②如图2,∠ADE=∠ABC=30°,①中的结论是否成立?请说明理由.
(2)在(1) ①的条件下,AB=6,AD=4,若把△ADE绕点A旋转,当∠EAC=90°时,画图并求PB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax-2x+c(a≠0)与x轴,y轴分别交于点A,B,C三点,已知点(-2,0),C(0,-8),点D是抛物线的顶点.
(1)求抛物线的解析式及顶点D的坐标;
(2)如图,抛物线的对称轴与x轴交于点E,第四象限的抛物线上有一点P,将△EB直线EP折叠,使点B的对应点B'落在抛物线的对称轴上,求点P的坐标;
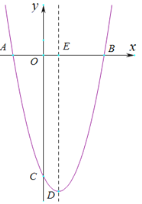
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业500名员工参加安全生产知识测试,成绩记为A,B,C,D,E共5个等级,为了解本次测试的成绩(等级)情况,现从中随机抽取部分员工的成绩(等级),统计整理并制作了如下的统计图:
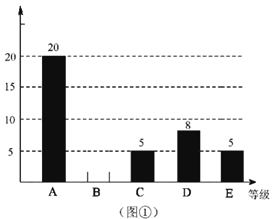
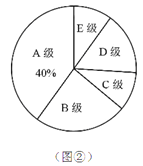
(1)求这次抽样调查的样本容量,并补全图①;
(2)如果测试成绩(等级)为A,B,C级的定为优秀,请估计该企业参加本次安全生产知识测试成绩(等级)达到优秀的员工的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C.
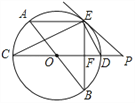
(1)求证:PE是⊙O的切线;
(2)求证:ED平分∠BEP.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,反比例函数![]() (x>0)与正比例函数y=kx、
(x>0)与正比例函数y=kx、 ![]() (k>1)的图象分别交于点A、B,若∠AOB=45°,则△AOB的面积是________.
(k>1)的图象分别交于点A、B,若∠AOB=45°,则△AOB的面积是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
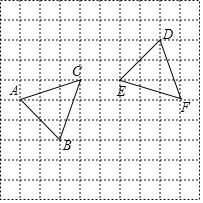
【题目】如图,在边长均为1的正方形网格纸上有![]() 和
和![]() ,顶点A、B,C,D、E、F均在格点上,如果
,顶点A、B,C,D、E、F均在格点上,如果![]() 是由
是由![]() 绕着某点O旋转得到的,点
绕着某点O旋转得到的,点![]() 的对应点是点D,点C的对应点是点
的对应点是点D,点C的对应点是点![]() 请按要求完成以下操作或运算:
请按要求完成以下操作或运算:
![]() 在图上找到点O的位置
在图上找到点O的位置![]() 不写作法,但要标出字母
不写作法,但要标出字母![]() ,并写出点O的坐标;
,并写出点O的坐标;
![]() 求点B绕着点O顺时针旋转到点E所经过的路径长.
求点B绕着点O顺时针旋转到点E所经过的路径长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com