
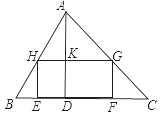
 有一块三角形的余料ABC,要把它加工成矩形的零件,已知,BC=12cm,高AD=8cm,矩形EFGH的边EF在BC边上,G、H分别在AC、AB上.
有一块三角形的余料ABC,要把它加工成矩形的零件,已知,BC=12cm,高AD=8cm,矩形EFGH的边EF在BC边上,G、H分别在AC、AB上.分析 (1)先由BC=12cm,高AD=8cm,HE=ycm、EF=xcm可知,AK=AD-y=8-y,HG=EF=x,再根据HG∥BC可知,△AHG∽△ABC,由相似三角形的对应边成比例即可得出y与x的函数关系式,根据x=y即可得出结论;
(2)根据(1)中的关系式用x表示出y,利用矩形及三角形的面积公式即可得出结论.
解答 解:(1)∵BC=10cm,高AD=8cm,HE的长为ycm、EF的长为xcm,四边形EFGH是矩形,
∴AK=AD-y=8-y,HG=EF=x,HG∥BC,
∴△AHG∽△ABC,
∴$\frac{AK}{AD}$=$\frac{HG}{BC}$,即$\frac{8-y}{8}$=$\frac{x}{12}$.
∵x=y,
∴x=4.8cm,即EF=4.8cm;
(2)∵由(1)可知,$\frac{8-y}{8}$=$\frac{x}{12}$,
∴y=8-$\frac{2}{3}$x.
∵矩形EFGH的面积是三角形ABC的面积的$\frac{1}{4}$,
∴xy=$\frac{1}{4}$×$\frac{1}{2}$×12×8=12,即(8-$\frac{2}{3}$x)x=12,解得x1=6+3$\sqrt{2}$,x2=6-3$\sqrt{2}$,
∴当EF长为6+3$\sqrt{2}$或6-3$\sqrt{2}$时,矩形EFGH的面积是三角形ABC的面积的$\frac{1}{4}$.
点评 本题考查的是相似三角形的应用,熟知相似三角形的对应边成比例是解答此题的关键.


 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:选择题
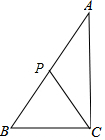 如图,△ABC是一个零件示意图,∠ACB=90°,AC=20cm,BC=15cm,从AB上取点P,与点C连结起来.以增加稳固程度.则PC的最小长度是( )
如图,△ABC是一个零件示意图,∠ACB=90°,AC=20cm,BC=15cm,从AB上取点P,与点C连结起来.以增加稳固程度.则PC的最小长度是( )| A. | 12cm | B. | 24cm | C. | 36cm | D. | 48cm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
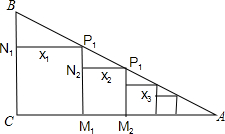 如图,在Rt△ABC中,∠C=90°,BC=a0,∠A=θ(其中a0,θ为常数),把边长依次为a1,a2,a3,…,a10的10个正方形依次放入Rt△ABC中,第一个正方形CM1P1N1的顶点分别放在Rt△ABC的各边上;第二个正方形M1M2P2N2的顶点分别放在Rt△AP1M1的各边上,…,其他正方形依次放入,则第10个正方形的边长a10=a0($\frac{1}{1+tanθ}$)10.(用a0,θ表示)
如图,在Rt△ABC中,∠C=90°,BC=a0,∠A=θ(其中a0,θ为常数),把边长依次为a1,a2,a3,…,a10的10个正方形依次放入Rt△ABC中,第一个正方形CM1P1N1的顶点分别放在Rt△ABC的各边上;第二个正方形M1M2P2N2的顶点分别放在Rt△AP1M1的各边上,…,其他正方形依次放入,则第10个正方形的边长a10=a0($\frac{1}{1+tanθ}$)10.(用a0,θ表示)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
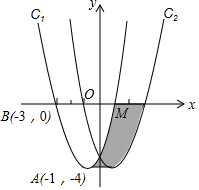 如图,在平面直角坐标xOy中,抛物线C1的顶点为A(-1,-4),且过点B(-3,0).
如图,在平面直角坐标xOy中,抛物线C1的顶点为A(-1,-4),且过点B(-3,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com