
【题目】如图,在矩形ABCD中,已知![]() ,
,![]() ,点P是边BC上一动点(点P不与点B,C重合),连接AP,作点B关于直线AP的对称点M,连接MP,作
,点P是边BC上一动点(点P不与点B,C重合),连接AP,作点B关于直线AP的对称点M,连接MP,作![]() 的角平分线交边CD于点N.则线段MN的最小值为_______________
的角平分线交边CD于点N.则线段MN的最小值为_______________

科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx﹣3交x轴于点A(﹣1,0)和点B(3,0),与y轴交于点C,顶点是D,对称轴交x轴于点E.

(1)求抛物线的解析式;
(2)点P是抛物线在第四象限内的一点,过点P作PQ∥y轴,交直线AC于点Q,设点P的横坐标是m.
①求线段PQ的长度n关于m的函数关系式;
②连接AP,CP,求当△ACP面积为![]() 时点P的坐标;
时点P的坐标;
(3)若点N是抛物线对称轴上一点,则抛物线上是否存在点M,使得以点B,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出线段BN的长度;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面给出六个函数解析式:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
小明根据学习二次函数的经验,分析了上面这些函数解析式的特点,研究了它们的图象和性质。下面是小明的分析和研究过程,请补充完整:
(1)观察上面这些函数解析式,它们都具有共同的特点,可以表示为形如![]() _______,其中x为自变量;
_______,其中x为自变量;
(2)如图,在平面直角坐标系![]() 中,画出了函数
中,画出了函数![]() 的部分图象,用描点法将这个函数的图象补充完整;
的部分图象,用描点法将这个函数的图象补充完整;

(3)对于上面这些函数,下列四个结论:
①函数图象关于y轴对称
②有些函数既有最大值,同时也有最小值
③存在某个函数,当![]() (m为正数)时,y随x的增大而增大,当
(m为正数)时,y随x的增大而增大,当![]() 时,y随x的增大而减小
时,y随x的增大而减小
④函数图象与x轴公共点的个数只可能是0个或2个或4个
所有正确结论的序号是________;
(4)结合函数图象,解决问题:若关于x的方程![]() 有一个实数根为3,则该方程其它的实数根为_______.
有一个实数根为3,则该方程其它的实数根为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.
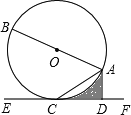
(1)求证:EF是⊙O的切线;
(2)求证:AC2=AD·AB;
(3)若⊙O的半径为2,∠ACD=300,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=![]() (m为常数且m≠0)的图象在第二象限交于点C,CD⊥x轴,垂足为D,若OB=2OA=3OD=6.
(m为常数且m≠0)的图象在第二象限交于点C,CD⊥x轴,垂足为D,若OB=2OA=3OD=6.

(1)求一次函数与反比例函数的解析式;
(2)求两个函数图象的另一个交点E的坐标;
(3)请观察图象,直接写出不等式kx+b≥![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年9月10日是我国第35个教师节,某中学德育处发起了感恩小学恩师的活动,德育处要求每位同学从以下三种方式中选择一种方式表达感恩:A.信件感恩,B.信息感恩,C.当面感恩.为了解同学们选择以上三种感恩方式的情况,德育处随机对本校部分学生进行了调查,井根据调查结果绘制成了如下两幅不完整的统计图.
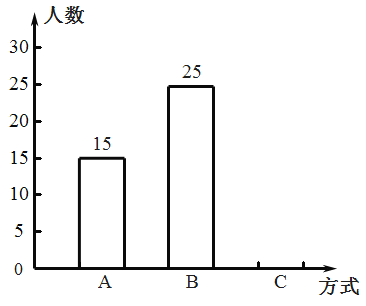
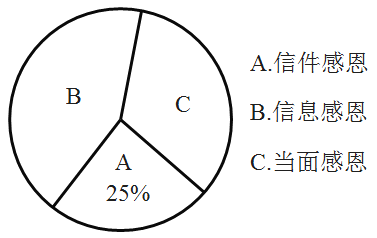
根据图中信息,解答下列问题:
(1)扇形统计图中C部分所对应的扇形圆心角的度数为________,并补全条形统计图;
(2)本次调查在选择A方式的学生中有两名男生和两名女生来自于同一所小学,德育处打算从他们四个人中选择两位在主题升旗仪式上发言,请用画树状图或列表的方法求恰好选到一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有4张分别标有数字2,3,4,6的扑克牌,除正面的数字外,牌的形状、大小完全相同.小红先从口袋中随机摸出一张扑克牌并记下牌上的数字为x;小颖在剩下的3张扑克牌中随机摸出一张扑克牌并记下牌上的数字为y,
(1)事件①:小红摸出标有数字3的牌,事件②:小颖摸出标有数字1的牌,则( )
A.事件①是必然事件,事件②是不可能事件,
B.事件①是随机事件,事件②是不可能事件,
C.事件①是必然事件,事件②是随机事件,
D.事件①是随机事件,事件②是必然事件,
(2)若|x-y|≤2,则说明小红与小颖“心领神会”,请求出她们“心领神会”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设中学生体质健康综合评定成绩为![]() 分,满分为100分,规定:
分,满分为100分,规定:![]() 为
为![]() 级;
级;![]() 为
为![]() 级;
级;![]() 为
为![]() 级;x<60为D级.现随机抽取某中学部分学生的综合评定成绩,整理绘制成如下两幅不完整的统计图,请根据图中的信息,解答下列问题:
级;x<60为D级.现随机抽取某中学部分学生的综合评定成绩,整理绘制成如下两幅不完整的统计图,请根据图中的信息,解答下列问题:

(1)在这次调查中,一共抽取了 名学生,![]() 级人数占本次抽取人数的百分比为
级人数占本次抽取人数的百分比为 ![]() ;
;
(2)扇形统计图中![]() 级对应的圆心角为 度;
级对应的圆心角为 度;
(3)若该校共有1000名学生,请你估计该校![]() 级学生有多少名?
级学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=8,sin A=![]()

(1)求AB的长;
(2)若点E在Rt△ABC的直角边上,点F在斜边AB上,当△CFE∽△ABC时,求CE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com