
【题目】已知:AB是⊙O的直径,点P在线段AB的延长线上,BP=OB=2,点Q在⊙O上,连接PQ.
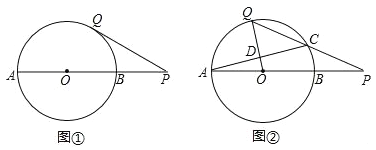
(1)如图①,线段PQ所在的直线与⊙O相切,求线段PQ的长;
(2)如图②,线段PQ与⊙O还有一个公共点C,且PC=CQ,连接OQ,AC交于点D.
①判断OQ与AC的位置关系,并说明理由;
②求线段PQ的长.
【答案】(1)![]() ;(2)①OQ⊥AC,理由见试题解析;②
;(2)①OQ⊥AC,理由见试题解析;②![]() .
.
【解析】试题分析:(1)如图①,连接OQ.利用切线的性质和勾股定理来求PQ的长度;
(2)如图②,连接BC.由三角形中位线得到BC∥OQ.利用圆周角定理得到BC⊥AC,故OQ⊥AC;
(3)利用割线定理来求PQ的长度.
试题解析:(1)如图①,连接OQ.∵线段PQ所在的直线与⊙O相切,点Q在⊙O上,∴OQ⊥OP.又∵BP=OB=OQ=2,∴PQ=![]() =
=![]() =
=![]() ,即PQ=
,即PQ=![]() ;
;
(2)OQ⊥AC.理由如下:如图②,连接BC.∵BP=OB,∴点B是OP的中点,又∵PC=CQ,∴点C是PQ的中点,∴BC是△PQO的中位线,∴BC∥OQ.又∵AB是直径,∴∠ACB=90°,即BC⊥AC,∴OQ⊥AC;
(3)如图②,PCPQ=PBPA,即![]() =2×6,解得PQ=
=2×6,解得PQ=![]() .
.



 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:
【题目】把下列各数分别填入相应的集合里.
﹣3.1415926,0, ![]() ,π,﹣
,π,﹣![]() ,
, ![]() ,﹣
,﹣![]() ,﹣1.414,
,﹣1.414, ![]() ,﹣0.2121121112…(每相邻两个2之间依次多一个1)
,﹣0.2121121112…(每相邻两个2之间依次多一个1)
有理数集合:{ …};
无理数集合:{ …};
负实数集合:{ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠B+∠BCD=180°,∠B=∠D.

求证:∠E=∠DFE.
证明:∵∠B+∠BCD=180°( 已知 ),
∴AB∥CD ( )
∴∠B=_______( )
又∵∠B=∠D(已知 ),
∴∠D=_______( )
∴AD∥BE( )
∴∠E=∠DFE( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂家新开发的一种电动车如图,它的大灯A射出的光线AB,AC与地面MN所夹的锐角分别为8°和10°,大灯A与地面离地面的距离为1m求该车大灯照亮地面的宽度BC.(不考虑其它因素)(参数数据:sin8°=![]() ,tan8°=
,tan8°=![]() ,sin10°=
,sin10°=![]() ,tan10°=
,tan10°=![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
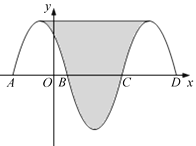
【题目】如图,抛物线y=﹣x2﹣2x+3与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1关于点B中心对称得C2,C2与x轴交于另一点C,将C2关于点C中心对称得C3,连接C1与C3的顶点,则图中阴影部分的面积为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
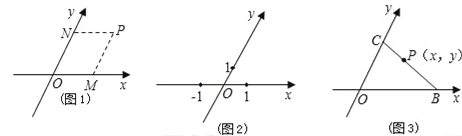
【题目】类似于平面直角坐标系,如图1,在平面内,如果原点重合的两条数轴不垂直,那么我们称这样的坐标系为斜坐标系.若P是斜坐标系xOy中的任意一点,过点P分别作两坐标轴的平行线,与x轴、y轴交于点M、N,如果M、N在x轴、y轴上分别对应的实数是a、b,这时点P的坐标为(a,b).
(1)如图2,在斜坐标系xOy中,画出点A(﹣2,3);
(2)如图3,在斜坐标系xOy中,已知点B(5,0)、C(0,4),且P(x,y)是线段CB上的任意一点,则y与x之间的等量关系式为 ;
(3)若(2)中的点P在线段CB的延长线上,其它条件都不变,试判断(2)中的结论是否仍然成立,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com