
 在第一象限内,以
在第一象限内,以| 5 |
| 1 |
| 2 |
| 5 |
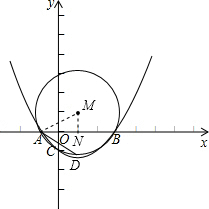 解:(1)∵A(-1,0),B(3,0),
解:(1)∵A(-1,0),B(3,0),| 1 |
| 2 |
| 1 |
| 2 |
| AM2-AN2 |
|
| (1-0)2+(1-y)2 |
| 5 |
|
|
| 1 |
| 3 |
| 2 |
| 3 |
| 5 |
| 5 |
| 1 |
| 3 |
| 2 |
| 3 |
| 5 |
| 5 |
| 5 |
| 5 |
2±
| ||||
| 2×1 |
7-3
|
7-3
|
| 5 |
7-3
|
| 5 |
| 5 |
| 1 |
| 3 |
| 2 |
| 3 |
| 5 |
| 5 |
| 5 |
| 5 |
2±
| ||||
| 2 |
1+3
|
1+3
|
| 5 |
1+3
|
| 5 |
7-3
|
| 5 |
7-3
|
| 5 |
1+3
|
| 5 |
1+3
|
| 5 |


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
 次连接起来形成一个图案(图案①).
次连接起来形成一个图案(图案①).查看答案和解析>>
科目:初中数学 来源: 题型:
| ||
| 3 |
| 3 |
| ||
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
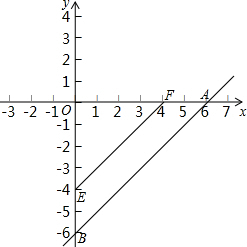 表达式,并求出S的最大值.
表达式,并求出S的最大值.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图图中的小方格都是边长为1的正方形,△ABC的顶点都在小正方形的顶点上,请完成以下题目
如图图中的小方格都是边长为1的正方形,△ABC的顶点都在小正方形的顶点上,请完成以下题目查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com