
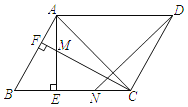
【题目】如图,在ABCD中,∠ACB=45°,AE⊥BC于点E,过点C作CF⊥AB于点F,交AE于点M.点N在边BC上,且AM=CN,连结DN.
(1)若AB=![]() ,AC=4,求BC的长;
,AC=4,求BC的长;
(2)求证:AD+AM=![]() DN.
DN.
【答案】(1)3![]() ;(2)见解析
;(2)见解析
【解析】
(1)证出△ACE是等腰直角三角形,由勾股定理得:AE=CE=2![]() ,BE=
,BE=![]() =
=![]() ,即可得出结果;
,即可得出结果;
(2)延长AD至G,使DG=AM,证出四边形CGDN是平行四边形,得出CG=DN,证明△ABE≌△CME,得出AB=CM,∠B=∠CME,再证明△ACM≌△GCD,得出∠G=∠MAC=45°,证出△ACG是等腰直角三角形,得出AG=![]() CG,即可得出结论.
CG,即可得出结论.
(1)解:∵∠ACB=45°,AE⊥BC,
∴∠AEC=∠AEB=90°,△ACE是等腰直角三角形,
∴∠EAC=45°,AE=CE=![]() =
=![]() =2
=2![]() ,
,
由勾股定理得:BE=![]() =
=![]() =
=![]() ,
,
∴BC=BE+CE=3![]() ;
;
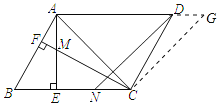
(2)证明:延长AD至G,使DG=AM,连接CG,如图所示:
∵AM=CN,
∴DG=CN,
∵四边形ABCD是平行四边形,
∴AB=CD,AD//BC,∠B=∠ADC,
∴DG∥CN,
∴四边形CGDN是平行四边形,
∴CG=DN,
∵CF⊥AB,
∴∠CFB=90°=∠AEB=∠CEA,
∴∠BAE=∠MCE,
在△ABE和△CME中,
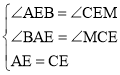 ,
,
∴△ABE≌△CME(AAS),
∴AB=CM,∠B=∠CME,
∴CM=CD,∠CME=∠ADC,
∴∠AMC=∠GDC,
在△ACM和△GCD中,
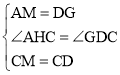 ,
,
∴△ACM≌△GCD(SAS),
∴∠G=∠MAC=45°,
∵AD//BC,
∴∠DAC=∠ACB=45°,
∴△ACG是等腰直角三角形,
∴AG=![]() CG,
CG,
∵AG=AD+DG=AD+AM,CG=DN,
∴AD+AM=![]() DN.
DN.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
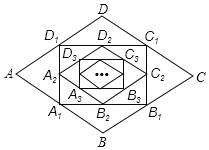
【题目】如图,在菱形ABCD中,边长为1,∠A=60,顺次连接菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去,…,则四边形A2019B2019C2019D2019的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是
是![]() 的反比例函数,下表给出了
的反比例函数,下表给出了![]() 与
与![]() 的一些值.
的一些值.
| … | -4 | -2 | -1 | 1 | 3 | 4 | … | ||
| … | -2 | 6 | 3 | … |
(1)求出这个反比例函数的表达式;
(2)根据函数表达式完成上表;
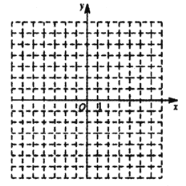
(3)根据上表,在下图的平面直角坐标系中作出这个反比例函数的图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 在
在![]() 轴正半轴上),
轴正半轴上),![]() 为等腰直角三角形,且面积为
为等腰直角三角形,且面积为![]() ,现将抛物线沿
,现将抛物线沿![]() 方向平移,平移后的抛物线过点
方向平移,平移后的抛物线过点![]() 时,与
时,与![]() 轴的另一点为
轴的另一点为![]() ,其顶点为
,其顶点为![]() ,对称轴与
,对称轴与![]() 轴的交点为
轴的交点为![]() .
.
![]() 求
求![]() 、
、![]() 的值.
的值.
![]() 连接
连接![]() ,试判断
,试判断![]() 是否为等腰三角形,并说明理由.
是否为等腰三角形,并说明理由.
![]() 现将一足够大的三角板的直角顶点
现将一足够大的三角板的直角顶点![]() 放在射线
放在射线![]() 或射线
或射线![]() 上,一直角边始终过点
上,一直角边始终过点![]() ,另一直角边与
,另一直角边与![]() 轴相交于点
轴相交于点![]() ,是否存在这样的点
,是否存在这样的点![]() ,使以点
,使以点![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 全等?若存在,求出点
全等?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应党和国家精准扶贫战略计划,某公司在农村租用了 720亩闲置土地种植了乔 木型、小乔木型和灌木型三种茶树. 为达到最佳种植收益,要求种植乔木型茶树的面积是小乔木型茶树面积的2倍,灌木型茶树的面积不得超过乔木型茶树面积的![]() 倍,但种植乔木型茶树的面积不得超过270亩. 到茶叶采摘季节时,该公司聘请当地农民进行采摘,每人每天可以采摘0.4亩乔木型茶叶,或者采摘0.5亩小乔木型茶叶,或者采摘0.6亩灌木型茶叶. 若该公司聘请一批农民恰好20天能采摘完所有茶叶,则种植乔木型茶树的面积是________亩.
倍,但种植乔木型茶树的面积不得超过270亩. 到茶叶采摘季节时,该公司聘请当地农民进行采摘,每人每天可以采摘0.4亩乔木型茶叶,或者采摘0.5亩小乔木型茶叶,或者采摘0.6亩灌木型茶叶. 若该公司聘请一批农民恰好20天能采摘完所有茶叶,则种植乔木型茶树的面积是________亩.
查看答案和解析>>
科目:初中数学 来源: 题型:
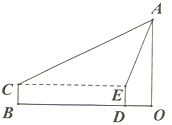
【题目】某中学为数学实验“先行示范校”,一数学活动小组带上高度为1.5m的测角仪BC,对建筑物AO进行测量高度的综合实践活动,如图,在BC处测得直立于地面的AO顶点A的仰角为30°,然后前进40m至DE处,测得顶点A的仰角为75°.
(1)求∠CAE的度数;
(2)求AE的长(结果保留根号);
(3)求建筑物AO的高度(精确到个位,参考数据:![]() ,
,![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线AC,BD相交于点O,E是CD的中点,连接OE.过点C作CF∥BD交线段OE的延长线于点F,连接DF.
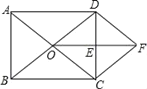
求证:(1)△ODE≌△FCE;
(2)四边形ODFC是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课外兴趣小组的同学们要测量被池塘相隔的两棵树A,B的距离,他们设计了如图的测量方案:从树A沿着垂直于AB的方向走到E,再从E沿着垂直于AE的方向走到F,C为AE上一点,其中4位同学分别测得四组数据:①AC,∠ACB;②EF,DE,AD;③CD,∠ACB,∠ADB;④∠F,∠ADB,FB.其中能根据所测数据求得A,B两树距离的有( )
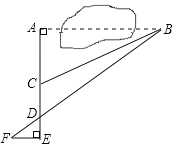
A.1组B.2组C.3组D.4组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,动点
,动点![]() 从点
从点![]() 出发,在
出发,在![]() 边上以每秒2
边上以每秒2![]() 的速度向点
的速度向点![]() 匀速运动,同时动点
匀速运动,同时动点![]() 从点
从点![]() 出发,在
出发,在![]() 边上以每秒
边上以每秒![]()
![]() 的速度向点
的速度向点![]() 匀速运动,设运动时间为
匀速运动,设运动时间为![]() (
(![]() ),连接
),连接![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() 与
与![]() 相似,求
相似,求![]() 的值;
的值;
(3)当![]() 为何值时,四边形
为何值时,四边形![]() 的面积最小?并求出最小值.
的面积最小?并求出最小值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com