
 勾股定理有着悠久的历史,它曾引起很多人的兴趣,如图所示,AB为Rt△ABC的斜边,四边形ABGM,APQC,BCDE均为正方形,四边形RFHN是长方形,若BC=3,AC=4,则图中空白部分的面积是
勾股定理有着悠久的历史,它曾引起很多人的兴趣,如图所示,AB为Rt△ABC的斜边,四边形ABGM,APQC,BCDE均为正方形,四边形RFHN是长方形,若BC=3,AC=4,则图中空白部分的面积是| AC2+BC2 |

|


科目:初中数学 来源: 题型:
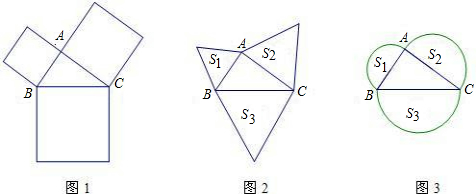
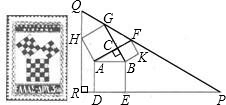
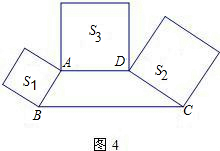 梯形外作正方形,其面积分别为S1、S2、S3,则S1、S2、S3之间的数量关系式为
梯形外作正方形,其面积分别为S1、S2、S3,则S1、S2、S3之间的数量关系式为查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 勾股定理有着悠久的历史,它曾引起很多人的兴趣.l955年希腊发行了二枚以勾股图为背景的邮票.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在上图的勾股图中,已知∠ACB=90°,∠BAC=30°,AB=8.作△PQR使得∠R=90°,点H在边QR上,点D,E在边PR上,点G,F在边PQ上,那么△PQR的周长等于
勾股定理有着悠久的历史,它曾引起很多人的兴趣.l955年希腊发行了二枚以勾股图为背景的邮票.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在上图的勾股图中,已知∠ACB=90°,∠BAC=30°,AB=8.作△PQR使得∠R=90°,点H在边QR上,点D,E在边PR上,点G,F在边PQ上,那么△PQR的周长等于| 3 |
| 3 |
查看答案和解析>>
科目:初中数学 来源:2011年河北省中考模拟试卷数学卷 题型:填空题
勾股定理有着悠久的历史,它曾引起很多人的兴趣.l955年希腊发行了二枚以勾股图为背景的邮票.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在右图的勾股图中,已知∠ACB=90°,∠BAC=30°,AB= 4.作△PQR使得∠R=90°,点H在边QR上,点D,E在边PR上,点G,F在边_PQ上,那么APQR的周长等于 ▲ 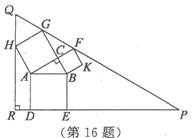

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com