
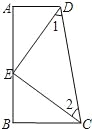
【题目】如图,AD∥BC,∠A=90°,E是AB上的一点,且AD=BE,∠1=∠2.
(1)Rt△ADE与Rt△BEC全等吗?请写出必要的推理过程;
(2)△CED是不是直角三角形?请说明理由;
(3)若已知AD=6,AB=14,请求出请求出△CED的面积.
【答案】(1)全等,见解析;(2)是,理由见解析;(3)50
【解析】
(1)由∠1=∠2,可得DE=CD,根据证明直角三角形全等的“HL”定理,证明即可;
(2)根据题意,∠AED+∠ADE=90°,∠BEC+∠BCE=90°,又∠AED=∠BCE,∠ADE=∠BEC,所以,∠AED+∠BEC=90°,即可证得∠DEC=90°,即可得出;
(3)由(1)可得BE=AD,所以可求出AE,根据勾股定理可求出DE,再由已知∠1=∠2和(2)可知)△CED是等腰直角三角形,从而求出△CED的面积
(1)Rt△ADE≌Rt△BEC;
理由如下:
∵∠1=∠2,
∴DE=CE,又∠A=∠B=90°,AE=BC
∴在Rt△ADE和Rt△BEC中,
DE=CE、AE=BC,
∴Rt△ADE≌Rt△BEC;
(2))△CDE是直角三角形;
理由如下:
∵Rt△ADE≌Rt△BEC,
∴∠AED=∠BCE,∠ADE=∠BEC,
又∵∠AED+∠ADE=90°,∠BEC+∠BCE=90°,
∴2(∠AED+∠BEC)=180°,
∴∠AED+∠BEC=90°,
∴∠DEC=90°,
∴△CDE是直角三角形;
(3)已知AD=BE=6,
∴AE=AB﹣BE=AB﹣AD=14﹣6=8,
在Rt△ADE中,
DE=![]()
![]() =10,
=10,
又∠1=∠2,
∴DE=CE=10,
再由(2)得:
△CED的面积为:![]() DECE=
DECE=![]() ×10×10=50.
×10×10=50.
所以△CED的面积为:50.
.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:
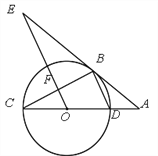
【题目】如图,CD为⊙O的直径,点B在⊙O上,连接BC、BD,过点B的切线AE与CD的延长线交于点A, ![]() ,OE交BC于点F.
,OE交BC于点F.
(1)求证:OE∥BD;
(2)当⊙O的半径为5, ![]() 时,求EF的长.
时,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】折纸的思考.
(操作体验)
用一张矩形纸片折等边三角形.
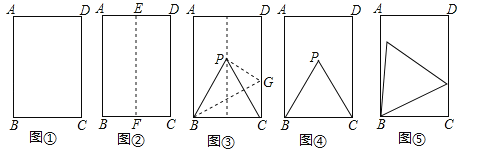
第一步,对折矩形纸片ABCD(AB>BC)(图①),使AB与DC重合,得到折痕EF,把纸片展平(图②).
第二步,如图③,再一次折叠纸片,使点C落在EF上的P处,并使折痕经过点B,得到折痕BG,折出PB,PC,得到△PBC.
(1)说明△PBC是等边三角形.
(数学思考)
(2)如图④,小明画出了图③的矩形ABCD和等边三角形PBC,他发现,在矩形ABCD中把△PBC经过图形变化,可以得到图⑤中的更大的等边三角形,请描述图形变化的过程.
(3)已知矩形一边长为3cm,另一边长为a cm,对于每一个确定的a的值,在矩形中都能画出最大的等边三角形,请画出不同情形的示意图,并写出对应的a的取值范围.
(问题解决)
(4)用一张正方形铁片剪一个直角边长分别为4cm和1cm的直角三角形铁片,所需正方形铁片的边长的最小值为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F.
(1)求证:四边形BEDF是平行四边形;
(2)当∠ABE为多少度时,四边形BEDF是菱形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A1(1,0),A2(1,﹣1),A3(﹣1,﹣1),A4(﹣1,1),A5(2,1),…则点A2017的坐标是( )
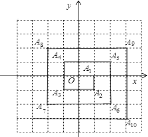
A.(505,504)B.(﹣503,﹣504 )C.(503,﹣503)D.(﹣504,504)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,我国很多地区持续出现雾霾天气.某社区为了调查本社区居民对雾霾天气主要成因的认识情况,随机对该社区部分居民进行了问卷调查,要求居民从五个主要成因中只选择其中的一项,被调查居民都按要求填写了问卷.社区对调查结果进行了整理,绘制了如下不完整的统计图表.被调查居民选择各选项人数统计表
雾霾天气的主要成因 | 频数(人数) |
A大气气压低,空气不流动 | m |
B地面灰尘大,空气湿度低 | 40 |
C汽车尾气排放 | n |
D工厂造成的污染 | 120 |
E其他 | 60 |
请根据图表中提供的信息解答下列问题:
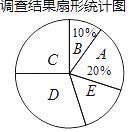
(1)填空:m=________,n=________,扇形统计图中C选项所占的百分比为________.
(2)若该社区居民约有6 000人,请估计其中会选择D选项的居民人数.
(3)对于“雾霾”这个环境问题,请你用简短的语言发出倡议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于数轴上的A、B、C三点,给出如下定义:若其中一个点与其它两个点的距离恰好满足2倍的数量关系,则称该点是其它两个点的“至善点”.例如:若数轴上点A、B、C所表示的数分别为1、3、4,则点B是点A、C的“至善点”.
(1)若点A表示数﹣2,点B表示数2,下列各数![]() 、0、1、6所对应的点分别为C1、C2、C3、C4,其中是点A、B的“至善点”的有 (填代号);
、0、1、6所对应的点分别为C1、C2、C3、C4,其中是点A、B的“至善点”的有 (填代号);
(2)已知点A表示数﹣1,点B表示数3,点M为数轴上一个动点:
①若点M在点A的左侧,且点M是点A、B的“至善点”,求此时点M表示的数m;
②若点M在点B的右侧,点M、A、B中,有一个点恰好是其它两个点的“至善点”,求出此时点M表示的数m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个正两位数的个位数字是a,十位数字比个位数字大2.
(1)列式表示这个两位数;
(2)把这个两位数的十位上的数字与个位上的数字交换位置得到一个新的两位数,试说明新数与原数的和能被22整除.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com